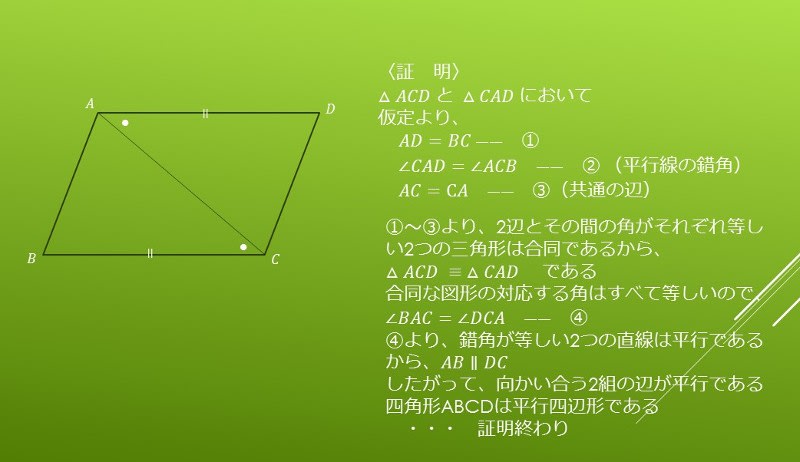
2年生 5 図形の性質と証明 知識・技能の習得を図る問題 年 組 号 氏名 全国学力・学習状況調査 A問題 ② 2 下のように「平行四辺形の2組の向かい合う辺はそれぞれ等しい」ことを証明しました。証明の基本は「直角三角形か正方形を複数個重ねる。」これだけ! 面白い証明方法としては「ユークリッドの証明」「相似を用いた証明」「内接円を用いた証明」などがある。 余弦定理を用いた証明は、循環論法なのでダメ 。図形の性質 例題(18) 練習問題 練習問題+解答 三角形の角の二等分線と比 メネラウスの定理,チェバの定理 円周角の定理(円に内接する四角形の性質) 接弦定理 方べきの定理 三垂線の定理数 学 ii 式と証明 例題(10) 練習問題 練習問題+解答複素数と方程式 例題(8)

中学2年数学 図形の調べ方 図形と証明 確認問題7 あんのん塾
図形の証明 合同
図形の証明 合同-⇒ 証明へ 加法定理より派生する公式 2倍角の公式,3倍角の公式,半角の公式,和積の公式,積和の公式,合成公式 加法定理の図形による理解 α < 90 ° , β < 90 ° , α β < 90 ° , 0 < α − β < 90 ° の場合について図形を用いて加法定理を理解する. 和の · 実は 「図形の証明問題」はさほど難しくはありません 。コツを掴むと「間違い探し」のような楽しい問題になるんですね。 そのためには、 図形の証明で使う最低限の知識(図形の性質、合同条件等)を頭に叩き込んで下さい。大した量ではありません。その後、「証明の書き方」を覚えます。
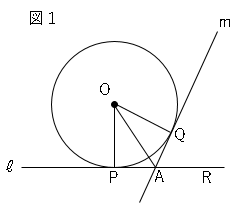



接線と円と合同の証明問題 数学の要点まとめ 練習問題一覧
· 中2数学図形の証明問題を攻略できる7つのコツ 図形の証明問題のコツを知りたい! こんにちは!この記事をかいているKenだよ。コーン、最高。 図形の証明問題 ってむずかしいよね。 図形の面積を計算する問題とは ちょっと違うタイプ。平面図形・証明 中学数学における最大の難関、それが「証明」です。 2つの三角形が合同であることを証明するという、産まれて初めての一大事です。 普通はじめてのことを学習するためには、1つ1つステップを踏んでいくのですが、 この「証明」は証明問題で二等辺三角形があるとき 証明問題で二等辺三角形があるとき、 どの \(2\) 辺が等しい二等辺三角形なのか、情報が与えられます。 そのとき、 「二等辺三角形なので、底角は等しい」 は証明なしで使ってOKです
問1,問2中2の図形証明分野習った後に解ける 問3相似習った後に解ける 芸術的な難問高校入試 第52回 「平行四辺形の超難しい証明」 出典:令和3年度 都立西高校(独自作成校) 過去問 数学 範囲:空間図形,相似,三平方の定理,難問 難易度:★★★★★★ 美しさ:★★★★★★ <問題 · 図形の証明問題 これは範囲としては「数学a」の分野で出題される可能性が高いです。 チェバの定理、メネラウスの定理を習うのが数学aなのでその定理に関係した問題が多いです。 また、大学入試でも証明問題は出題されます。問題例としては「辺abと辺cd数学の証明が驚くほどできるようになる4つのコツ! 証明問題は避けて通れないが、苦手とする受験生は多い。 普通に方程式を解いたり、積分をしたりといった計算は得意なのに、証明問題になると急に手こずってしまうのだ。 自分で方針を立て、論理をわかりやすく説明する。 そのためには、 計算力や思考力以外の力 が必要である。 そして、その力は数日で
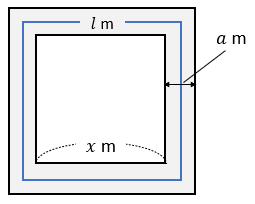
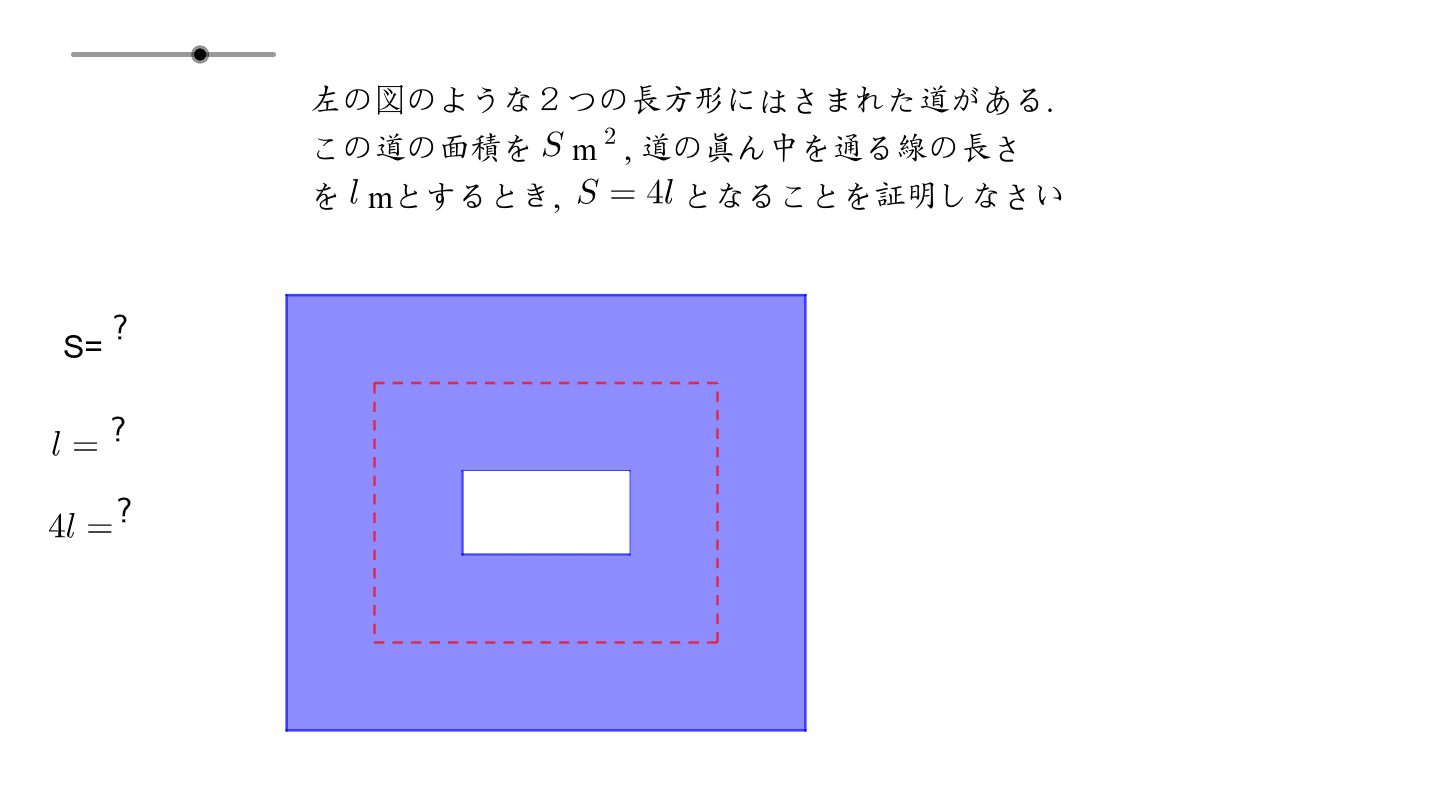
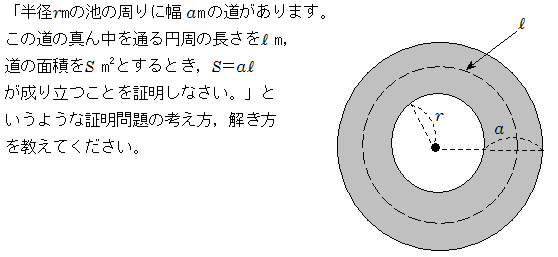
式を問題文 の語句を使って表しましょう。 S=alを証明すると,教科書のようになり ます。 この証明をよく読んで,意味が分か らないところに下線を引きましょう。 S=alは,土地の形が円でなくても成り立ちます。 正方形でも成り立つことを証明しましょう。 この道の真ん中を通る線の長さlmを式で表すと l=4x+πa・・・① 一方,この道の面積Sを式で表すと S · 多くの人にとって、証明という言葉に最初に出会うのは、中学の数学、図形(幾何)の問題ではないでしょうか。三角形の合同条件や相似条件ですね。高校数学では、 背理法を使った証明を習うでしょう。 図に示された2つの三角形がある。その2辺とその間の角がそれぞれ等しいから、こ今回は、中2で学習する証明問題の単元から 平行四辺形の証明問題について取り上げていくよ! 平行四辺形の証明問題とは、大きく分けて以下の2つだね 平行四辺形の性質を利用した合同の証明 平行四辺形になることを証 図形と証明 直角三角形の合同条件証明問題の書き方とは? イチから徹底解説! kaztastudy 今回は中2で学習する図形の単元から
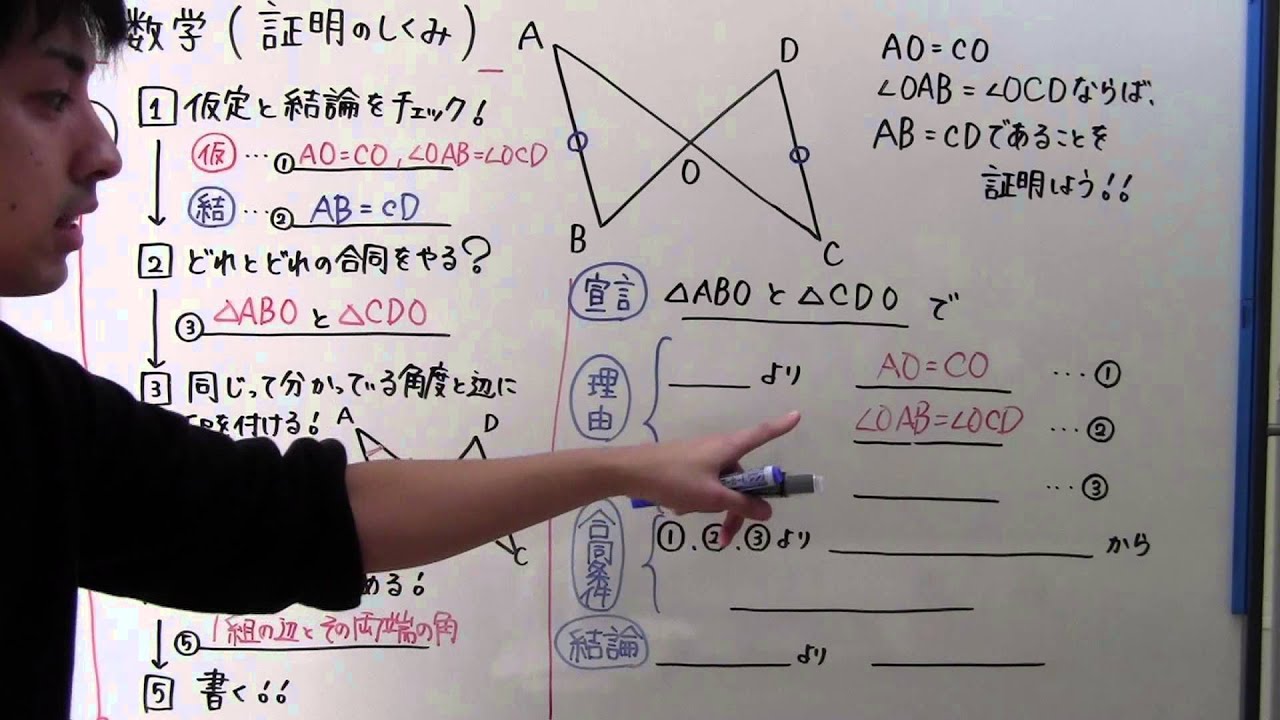



中2 数学 中2 60 証明のしくみ Youtube




直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ
≪図形の証明のコツ≫ 証明の仕方を覚えるとしても,それを応用できなければ,実際に問題を解くことに結びつきません。 なので, ・似た問題を見つけて,証明の解答の書き方をまねする →よく出てくる証明のパターンをつかむ数学Aの平面図形で使う定理の一覧 三角形の角の二等分線と辺の比 三角形ABCにおいて、∠BACを二等分する線とBCとの交点をDとしたとき、次の定理が成り立つ。 角の二等分線と辺の比の証明 三角形の外角の二等分線と辺の比 AB相似な図形の面積 相似な立体の表面積・体積(1) 相似な立体の表面積・体積(2) 6 円 円周角と中心角(1) 問題一括 (2,462Kb) 解答一括 (2,734Kb) 円周角と中心角(2) 円周角と中心角(3) 等しい弧と円周角 円周角と図形の証明 円周角の定理の逆 円周角の定理の活用 7




急ぎです W 中2の数学 図形の証明です Clear




三角形の合同条件 合同の証明問題と解き方のコツ リョースケ大学
· 図形の証明の発想にもっと慣れたい人は、私(朝倉幹晴)が執筆し、アマゾンでも販売している、図形三部作「円」「三角形」「図形の証明」のうち、特に「図形の証明」(税込み330円)を読んでみてください。 アマゾン取り扱い、朝倉幹晴著書一覧 朝倉幹晴をフォローする @asakuramikiharu · これこそが、図形問題なのである。 測ったらタルトが本当に45度で切られていて見事だった 肩慣らしとして、これを解いてみよう。 出題は、「xの角度を求めよ」。 三角形の内角の和は180度。 かつタルトは二等辺三角形なので、角ABCは (180度45度)/2 = 675・平行四辺形の性質を利用して、図形の証明をすることができる。 ・証明の結果からわかった、新たな性質を理解することができる。 (2)本時の指導について 本時の授業では、関連づけを図る(別の場面に置き換える)課題を扱い、平行四辺形の性質




中2数学 三角形の合同の証明の解き方の手順 こいがくぼ翼学習塾




これで点が取れる 単元末テスト中2数学 5章 図形の性質と証明
動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru平面図形・証明 » 中学数学証明・二等辺三角形の性質の利用 ;三角形 三角形の合同条件 三角形の合同条件2 三角形の合同の証明 基本問題1 三角形合同の証明1 三角形の合同証明2 三角形の合同証明3 三角形の合同証明4 三角形の合同証明5 平行線の証明 三角形の合同証明6 二等辺三角形 二等辺三角形の性質 二等辺三角形2 直角三角形1 直角三角形2 直角三角形3




中3数学 図形と相似9 相似条件と証明 折り返しの図形 すべて無料 星組の中学数学講座




中2数学 証明とは 練習編 映像授業のtry It トライイット
単元:4章 図形の調べ方(2節 証明) 指導計画 1.証明とそのしくみ・・・2時間(本時第1時・第2時) 2.合同条件を使った証明の進め方・・・2時間;2年生 5 図形の性質と証明 (2) 花子さんは,四角形ADPEが平行四辺形になることを証明しました。証明を完成させなさい。 四角形ADPEで,仮定より, DP//AE ① (3) 太郎さんと花子さんは,お互いの証明を見て,あることに気付きました。2人の証明から分か図形の証明の学習における論証の意義と考え方に関する研究 数学教育専修 千 﨑 創 都 1.研究の動機、目的、方法 中学校数学科図形領域の証明問題で次の二点で感じたことがある。
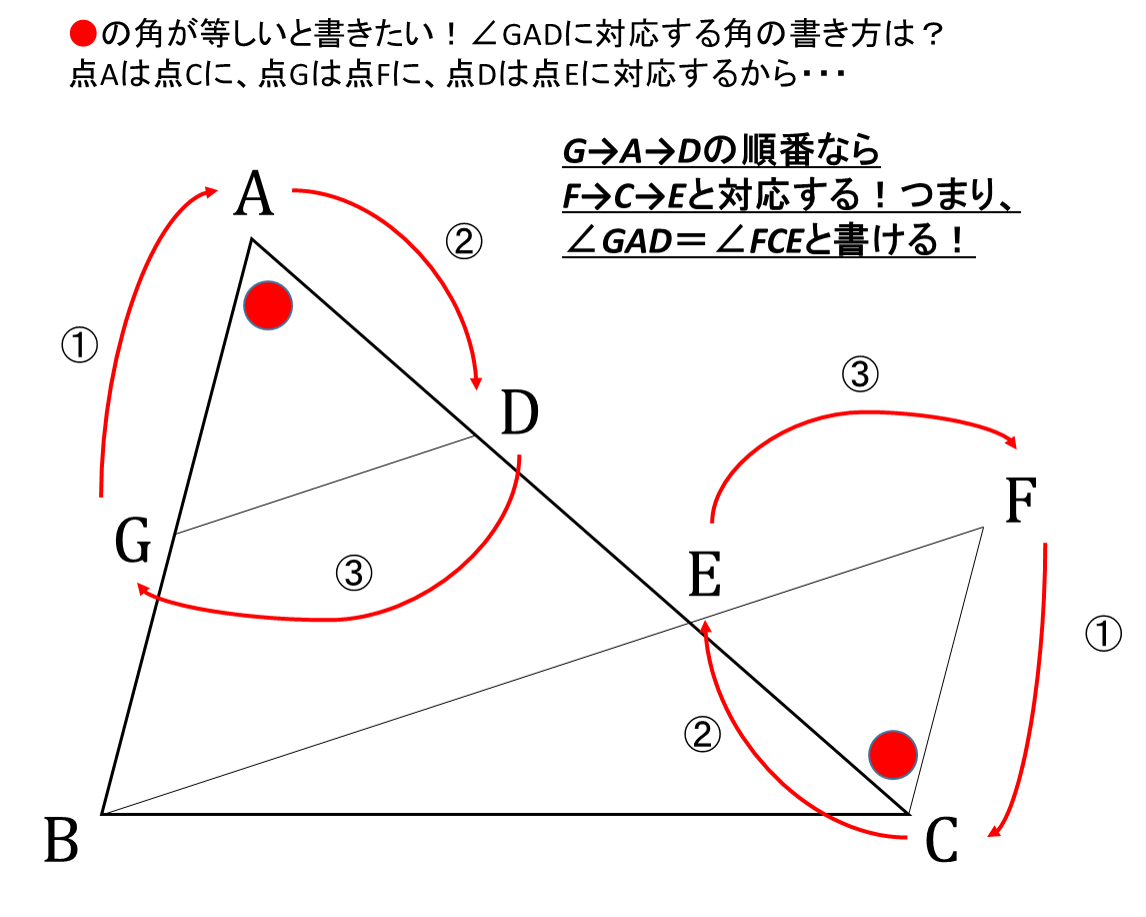



数学 中学証明問題を解く4つのポイント
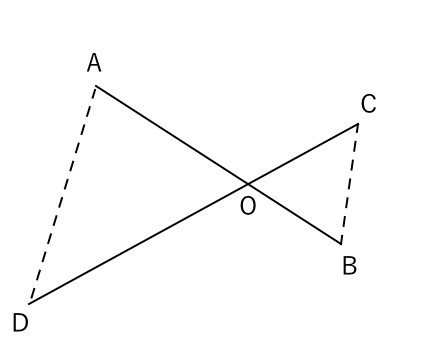



相似な図形 証明に慣れよう 苦手な数学を簡単に
· 図形の証明は苦手にしている人が多い単元ですが、 入試でも必ずと言っていいほど出題される問題 でもあります。しっかりと練習を積めばできるようになりますし、部分点などももらうことができて比較的点数をとりやすいところでもあります。教科書などを見ながらでも取り組んでみて · 中学2年生の数学では、図形の合同,三角形の合同条件, 証明 を習いますよね? 証明問題は、新潟県の高校入試にも必ず出題されますが、 苦手な中学生がとても多い です。 中には、証明が出てきただけで、全く手がつけられずにギブアップという中3受験生も。 。 。 新潟県公立高校入試数学の証明問題は、難しい年もありますが、最近は点数の取りやすい円の図形による証明 半径 mの円の周囲に,幅 mの道がある。 この道の面積を ㎡,道の真ん中を通る円周の長さを mとするとき, であることを証明しなさい。 まずは、大きな円から小さい円を取り除いて道の面積Sを求めましょう。 今回は円なので、半径の大きさに注目しながら面積を求めてくださいね。 円の面積を忘れていた人は喝だッ! しっかりと思い出し



中2数学 図形の証明問題では様々な図形の性質を理解することが大切 中学生 受験対応 英語 数学 学習講座




19年2月25日 数学 図形の証明問題 オンライン家庭教師 ウェブリー
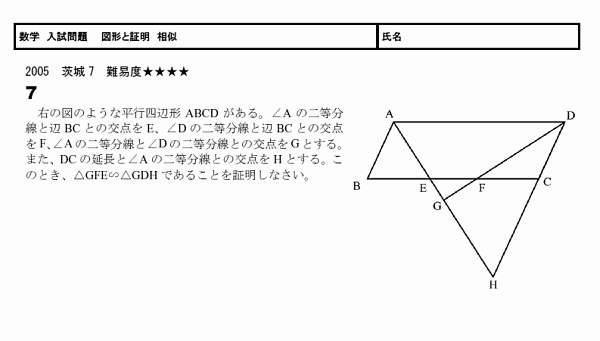
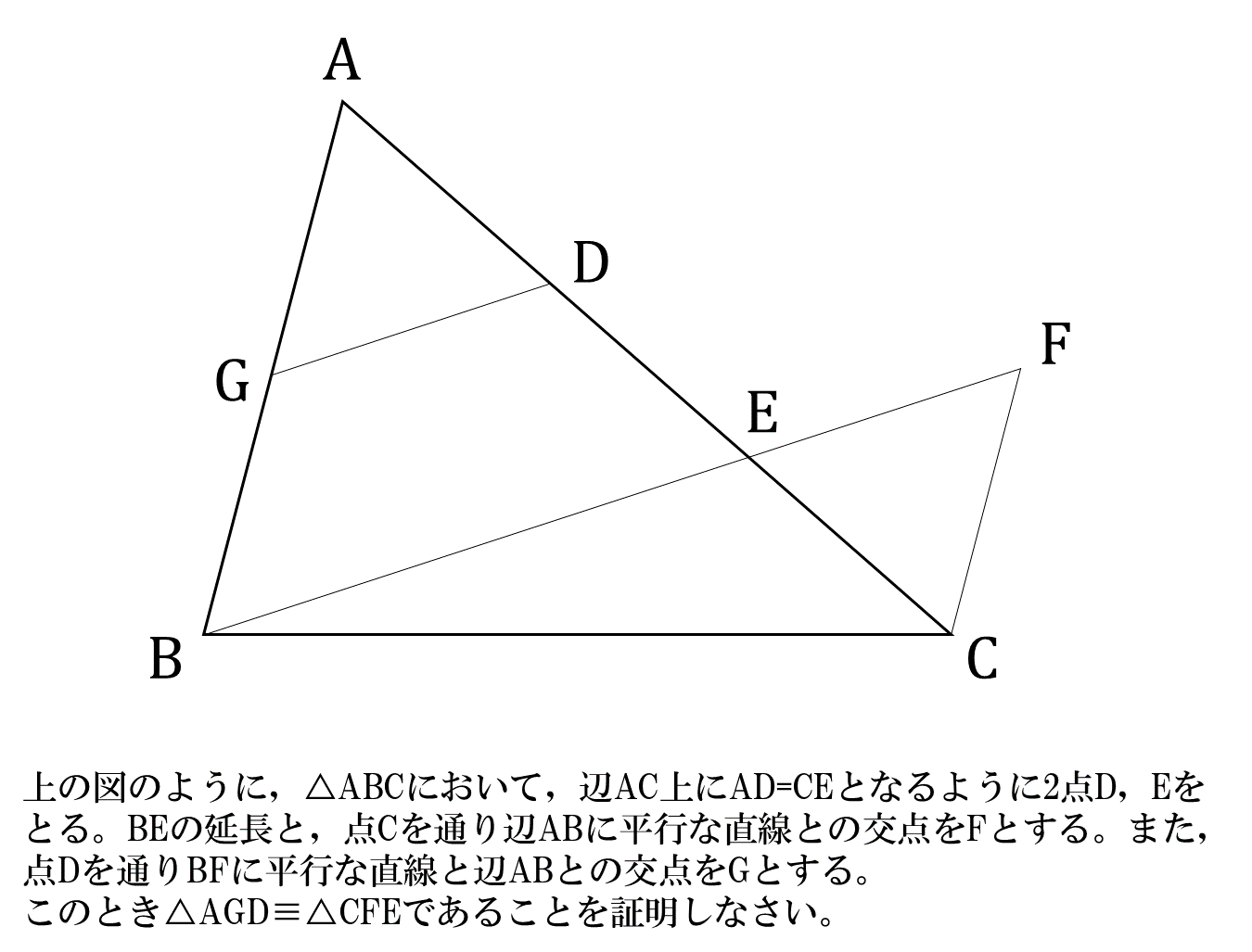
1年 比例反比例の応用 4 問題文 PがAを出発してからx秒後 (誤) PがBを出発してからx秒後 (正) 2年 連立方程式 解と係数 (1)問題, (3)答b=5 (誤) b=3 (正) 1年 文字式の計算2 (加減)3③答 17 a → − 17 a 2年 角度2 3③130°→131° 3年 放物線と図形1 5 (3)解答 (0,4)→ (0,42.証明の意義 中学校2年生の図形領域で生徒が学ぶ図形 は、小学校において既にその内容のほとんど134が実測や実験という方法で学習されている。 それゆえ、証明の意義の指導なしには、生徒 は証明という新たな追求方法を必要であると は思わないと推測される。 そこでまず、証明の意義3結論を見て、覚えた図形の条件のどれを使うか決める 図形の条件とは「三角形の合同条件」「三角形の相似条件」のことです。 問題文の仮定、結論、図をじっくりみてどの条件を使うか考えましょう。 この例題では 2でも書いた通り、結論は「 AGD≡ CFE」、仮定は「AD=CE」「AB∥CF」「GD∥BF」ですよね。 まず合同を証明するので、 ①3辺がそれぞれ等しい ②2
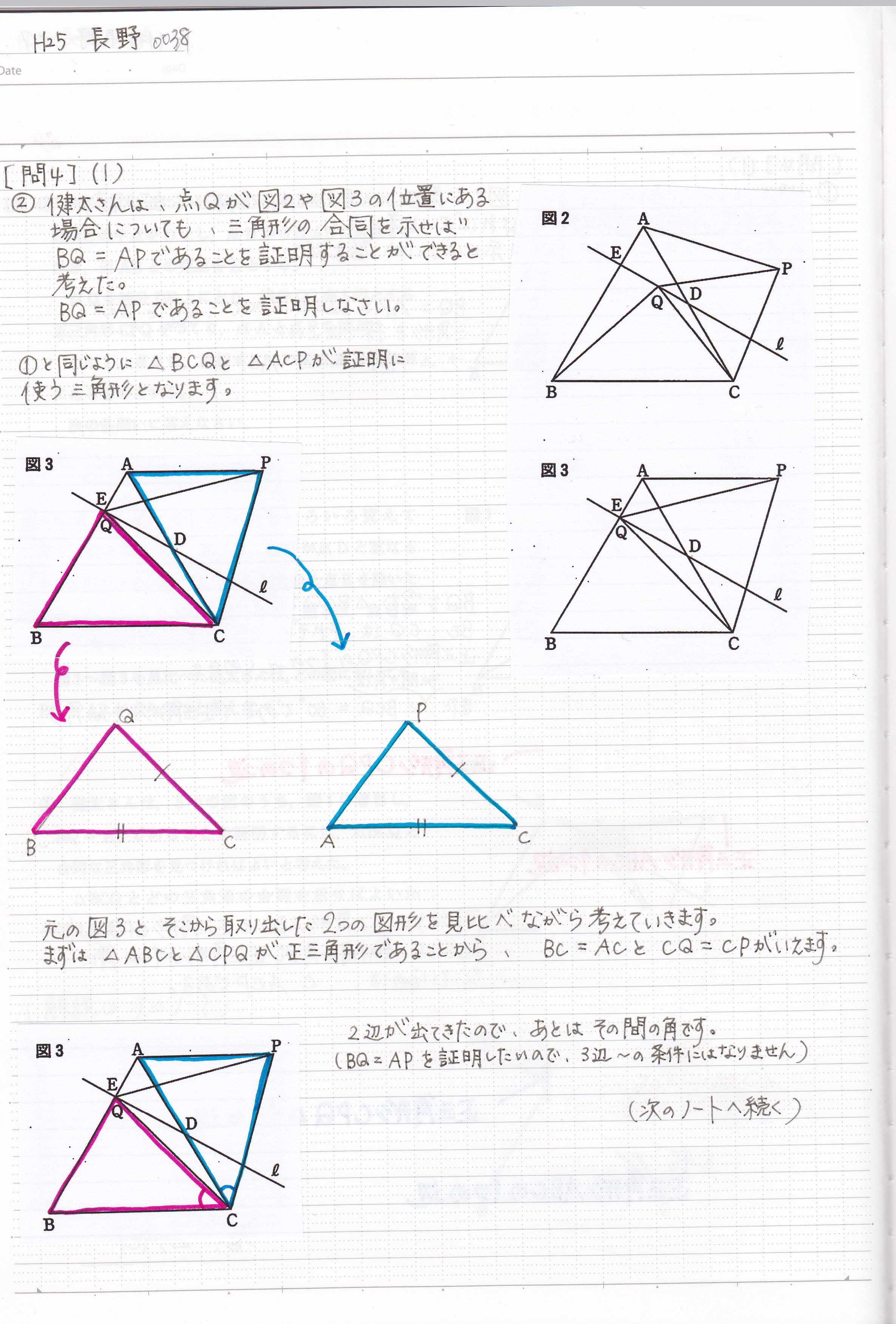



平成25年長野県立高校 入試問題 図形の証明問題 合同 現役塾講師のわかりやすい中学数学の解き方
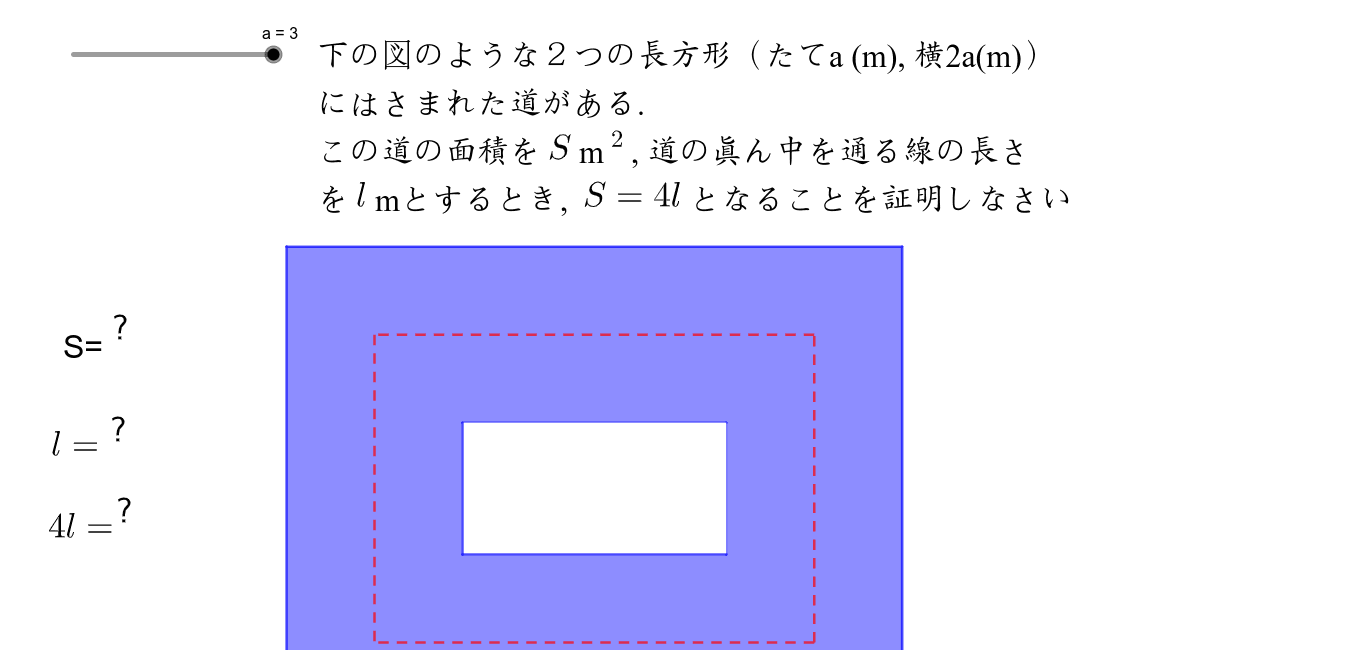



式の計算の利用 図形の証明2 Geogebra
· 公式・証明から計算問題まで解説 三平方の定理、あなたはちゃんと説明できますか?問題、解けますか? 中学数学の中でも、図形問題はなかなか難しいものの1つです。三平方の定理は、その図形問題を解く際の基礎であり、必要不可欠な知識で(証明)両辺を展開し、共通な項を消去すると、補題3と一致する。(証明終り) ②と①は「+を×に、×を+に置き換え、不等号の向きを逆にした」関係にある。 補題3は、再配列不等式と呼ばれるもののもっとも単純な場合であり、それについて 補題4のような双対が存在するどの三角形の合同を証明すべきか(17年度北海道) このブログは「図がシンプルだけど結構キツイ問題」を紹介する目的で最初は作りました。 だんだん色々な問題を紹介するようになりましたが。 今回は,初心に戻って,非常に図がシンプルだけど,何




中2 図形の証明です g Cbg Cgb 90 Clear




メルカリ 中学数学 図形の証明がらくらく解ける 参考書 444 中古や未使用のフリマ




接線と円と合同の証明問題 数学の要点まとめ 練習問題一覧




メルカリ 中古理由あり 中学数学図形の証明がらくらく解ける 参考書 400 中古や未使用のフリマ
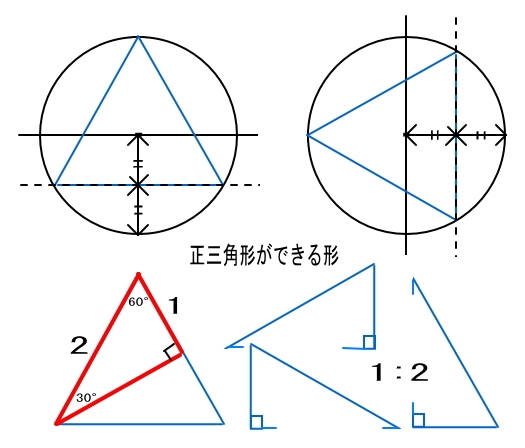



図形の証明に正三角形を作図 2 齊藤数学教室 算数オリンピックから大学数学入門



中2数学 基本解説プリント12 図形6 証明のしくみと根拠 問題 226



図形と証明 相似 無料学習プリント教材
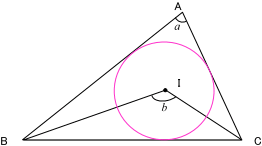



図形の証明の考え方 数学 苦手解決q A 進研ゼミ高校講座
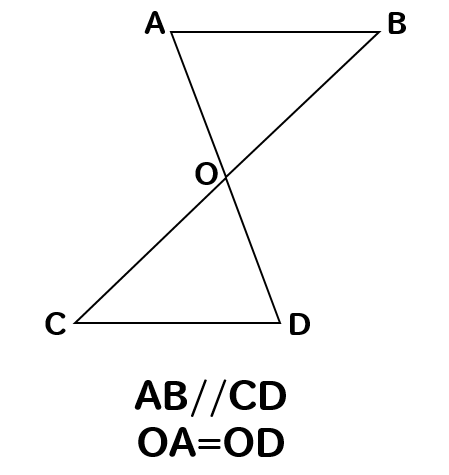



証明の書き方 合同な三角形の証明問題のかき方を基礎から解説 数スタ




中学数学 図形の証明問題の解き方 すごく苦手な人もok なぜか分かる はかせちゃんの怪しい研究室




高校数学a 三角形の内角 外角の二等分線と辺の比の関係とその証明 受験の月
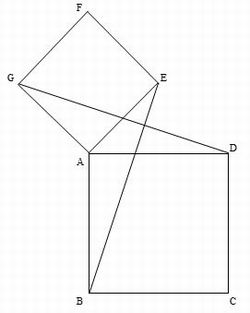



入試対策 図形の証明問題は意外と簡単だ 駿英式 勉強術
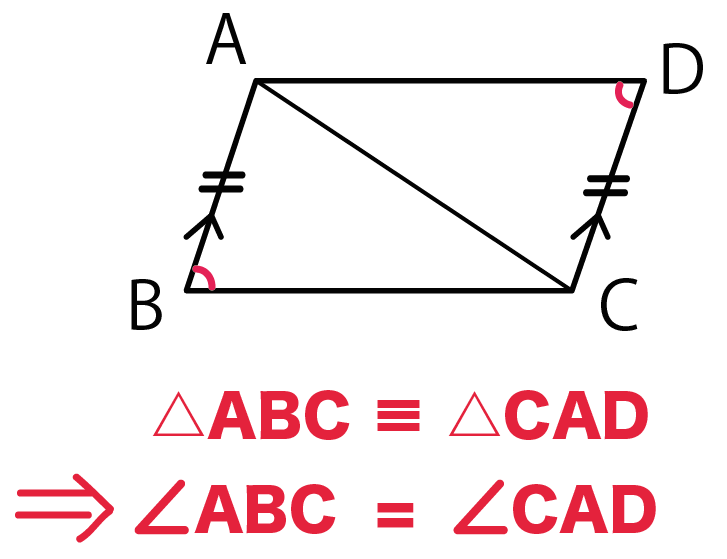



中2数学 図形の証明問題を攻略できる7つのコツ Qikeru 学びを楽しくわかりやすく




図形に関する性質の証明 身勝手な主張




数学 中3 14 式の計算の利用 図の証明編 Youtube



合同な図形 三角形の証明問題 苦手な数学を簡単に



図形の総合問題の解き方 合同証明 三平方の定理 相似など 現役塾講師のわかりやすい中学数学の解き方




中学数学 相似な図形の証明問題のコツ ちょい難問 なぜか分かる はかせちゃんの怪しい研究室




中学数学図形の証明がらくらく解ける の通販 紙の本 Honto本の通販ストア




中2数学 図形の調べ方 中学生 数学のノート Clear




平行四辺形の証明問題 無料で使える中学学習プリント




図形の証明問題を教える工夫




図形に関する性質の証明 身勝手な主張




Paypayフリマ かずお式中学数学ノート 中2 図形と証明




中学生 合同な図形と証明のノート一覧 Clear



図形の証明 合同 現役塾講師のわかりやすい中学数学の解き方




問題形式で味わう 補助線の魅力 考えて楽しむ図形の証明 株 現代図書 オンラインストア



中3 式の計算の利用 円 正方形の図形の証明をイチから 数スタ




平行四辺形の証明問題 無料で使える中学学習プリント




中学 数学 実力テスト 過去問 平面図形と証明 問題と解答 赤城 ᴗ




この様な中学二年生で習う 応用問題である証明問題での質問です この証明問題は Clear
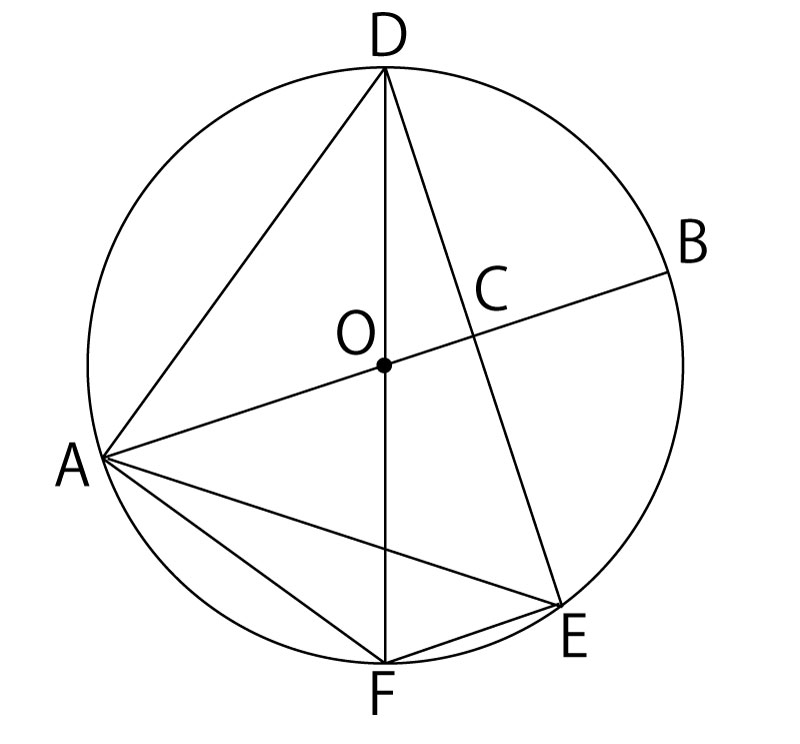



16年前期 千葉県公立高校入試 数学 第4問 図形の証明 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




こわくない数学 図形の証明問題 くもん出版
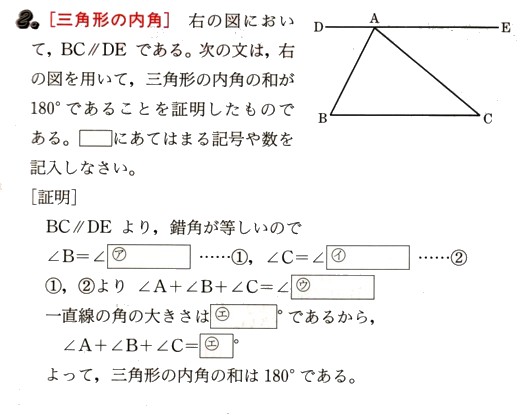



中学2年数学 図形の調べ方 図形と証明 練習問題2 あんのん塾




三角形の合同条件と証明問題の解き方 数学fun



3




2が無理数であることの図形的な証明 理系のための備忘録




中学2年数学 図形の調べ方 図形と証明 確認問題7 あんのん塾




18年千葉県公立高校入試 前期 数学第4問 図形の証明 問題 解答 解説 18年2月13日実施 船橋市議会議員 朝倉幹晴公式サイト




14年前期 千葉県公立高校入試 数学 第4問 図形の証明 配点15点 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




全都道府県 公立高校入試 過去問 数学 4 平面図形 3 合同の証明ほか 在宅学習で高校受験対策
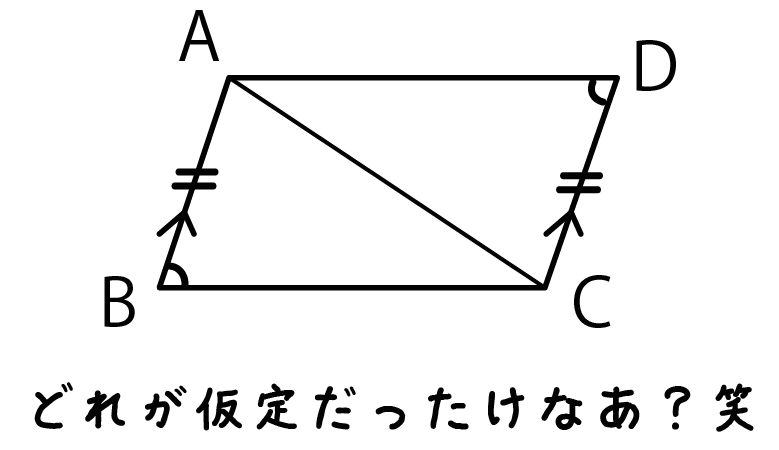



中2数学 図形の証明問題を攻略できる7つのコツ Qikeru 学びを楽しくわかりやすく




中学2年生 数学 合同と証明 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




超 パワーアップ中学数学 図形の証明 中継点 文字式の表現 活用テクニック Myisbn デザインエッグ社 長通 幸大 本 通販 Amazon



図形の証明のこれくらいの問題は自由記述でテストに出ますか 証明の問題は Yahoo 知恵袋
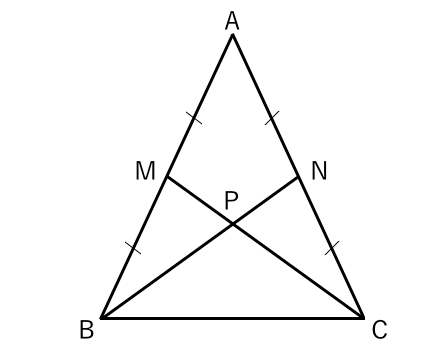



合同な図形 二等辺三角形の証明問題 苦手な数学を簡単に




Ab Abcdfrac12abtimesce Descubre Como Resolverlo En Qanda
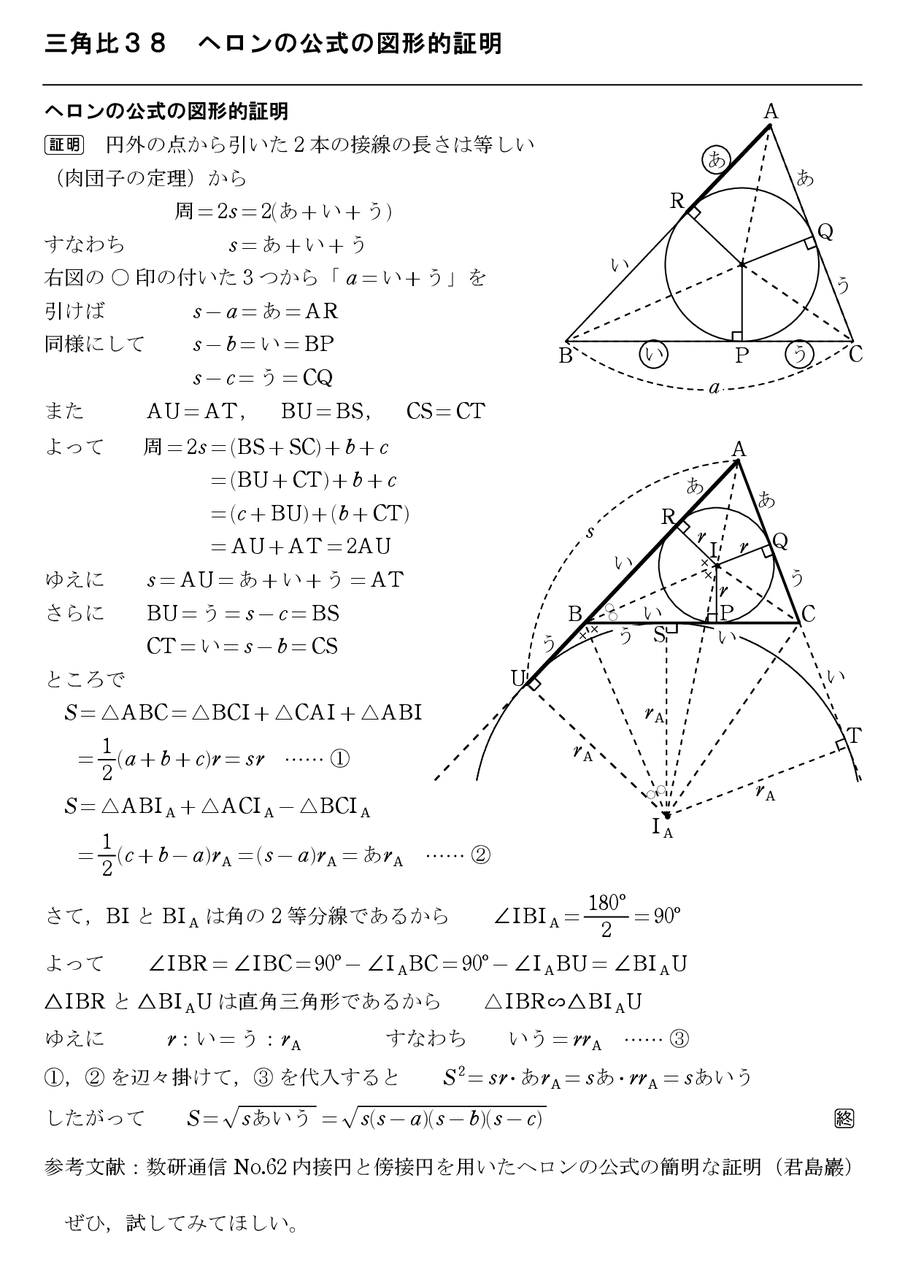



三角比38 ヘロンの公式の図形的証明 怜悧玲瓏 高校数学を天空から俯瞰する




高校数学 中線定理の5通りの証明 図形を扱う5分野の解法比較 受験の月




中学数学 証明は簡単 合同な図形を探すたった1つのポイント 烈志塾 塾長ブログ



Q Tbn And9gctfnzfy41m Mb9nzbmrxfsaq84jm0k9vzrzk4aserqyecy4vtso Usqp Cau



2
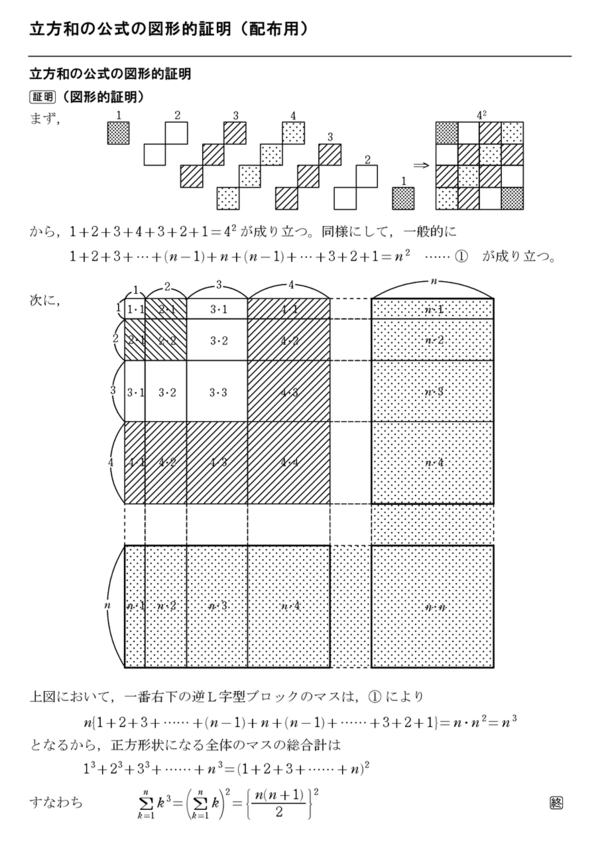



立方和の公式の図形的証明 配布用 怜悧玲瓏 高校数学を天空から俯瞰する
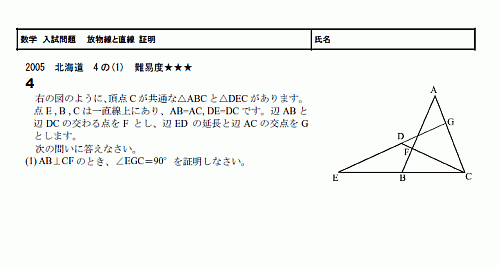



図形と証明 相似 スタディーx



式の計算の利用 図形の証明 Geogebra



1



数学 中学証明問題を解く4つのポイント




図形に関する性質の証明 身勝手な主張



19年前期 千葉県公立高校入試 数学 第4問 図形の証明 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




世界一わかりやすい数学問題集中2 5章 図形の性質と証明




図形を中学レベルで教えてみた




中2数学 図形の性質と証明 1 2 二等辺三角形 1 Youtube




図形の証明問題です 全く分かりません 分かる方教えてください Clear
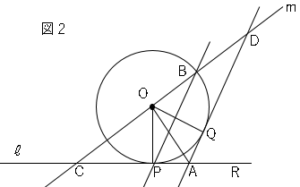



接線と円と合同の証明問題 数学の要点まとめ 練習問題一覧




図形の証明はムズカシイ ニート戦記



図形の証明に正三角形を作図 1 齊藤数学教室 算数オリンピックから大学数学入門




ม 2 โน ตของ 数学 中2 図形の性質と証明 ช น Junior Clear



Studydoctor図形の性質と相似の証明 中3数学 Studydoctor




苦手な人が多い図形の証明問題を解くコツを解説 実は非常に簡単なんです 学習塾 Step By Step




メルカリ 中学数学図形の証明がらくらく解ける 参考書 399 中古や未使用のフリマ




数学 やる意味あるの あります 図形の証明問題にチャレンジ 東京 江東区猿江 住吉の少人数指導学習塾 ほっとすぺーすかたつむりのブログ 不登校 学習の遅れ 軽度発達障害にも対応




図形の証明のにがてな人へ 理社出版編集部 本 通販 Amazon




数学 中3 46 相似の証明チャレンジ Lv 1 Youtube



合同な図形の証明練習 個人塾 個人指導の教材



図形と証明 相似 スタディーx



中学数学 三角形の合同の証明 その2 中学数学の無料オンライン学習サイトchu Su




中2数学 証明とは 例題編 映像授業のtry It トライイット




心に強く訴える数学 図形 証明 最高のぬりえ



中2数学 発展問題プリント12 図形6 証明のしくみと根拠 問題 226



中2数学 図形の証明 Eccジュニアbs小机教室 横浜港北区 子ども 大人英語英会話



式の計算 式による図形の証明問題の解き方のコツ 中学数学 定期テスト対策サイト




メルカリ 図形の証明のにがてな人へ 中学生用 参考書 300 中古や未使用のフリマ
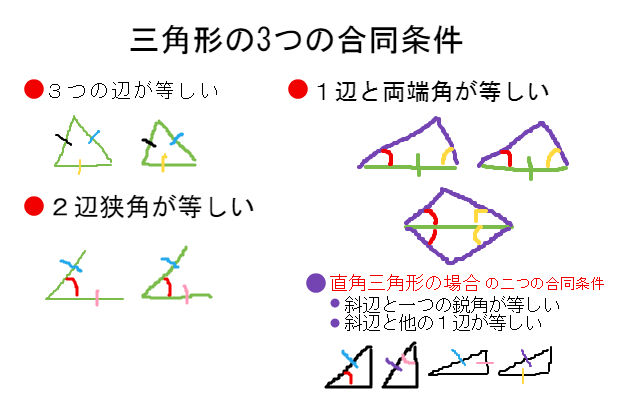



図形の証明問題に必要な最低限の知識 中学数学 理科 寺子屋塾の復習サイト




中学2年生の数学 証明 三角形の合同条件と証明の書き方 塾講師が数学をやりmath



1
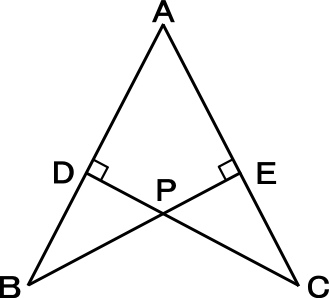



中学2年数学練習問題 図形と合同 三角形の合同の証明問題




1研究中 C 数学11 図形の証明 合同 相似 合同式 Mod余りの数 チェバの定理メネラウスの定理
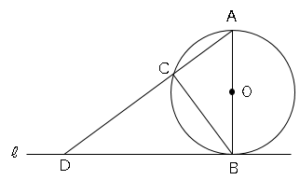



円が2つある相似の証明問題と面積を求める問題 数学の要点まとめ 練習問題一覧




メルカリ 中学 数学 図形の証明がらくらく解ける 参考書 300 中古や未使用のフリマ



中2数学 図形の証明問題を攻略できる7つのコツ Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿