En los triángulo notable existe una relación conocida entre sus lados y ángulos Los triángulos notables son de 37°, 53°, 45°, 74°,76°, 30°, 60° entre otros Triangulo Triángulo Rectángulo Triángulos Notables Triángulo Notable de 15° y 75°Ejercicio donde aplicaremos las propiedades del triángulo notable 15°75°, triángulos isósceles, medianas y bisectrices#notable #triangulo #bisectriz #media15°, 30°, 45° y 60° En base a ésta información, uno puede calcular en forma exacta, los valores de las funciones seno y coseno cada 15° Analizando el primer cuadrante, tenemos los valores exactos de 15°, 30°, 45°, 60° y 75° Hay que notar que para el ángulo de 75°, puede ser generado por la suma de 30° más 45°

Todo Los Triangulos Notables Sus Angulos Medidas
Triángulo notable de 15 y 75 grados
Triángulo notable de 15 y 75 grados- About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us CreatorsA) 10 b) c) d) 15 e) 12 14 9 4 Se tienen tres circunferencias tangentes exteriores dos a dos en A, B y C respectivamen te, de modo que las prolongaciones de BA y BC intersecan a una de ellas en P y Q respectivamen te AQ y CP se intersecan en O ¿Qué punto notable es O del triángulo PBQ?




Congruencia De Triangulos Profesor De Matematica Facebook
Osea cuanto es el 15%= 8 se vende un carro 75´5000 solo hoy el almacen tiene el 8% de descuento Cuanto es el ahorro? Jesus Mendez Leer Teoría Triángulo Notable de 15° y 75° previous Razones trigonométricas de ángulos notables Parte II next Triángulo Notable El triángulo notable de 30 y 60 (treinta y sesenta), este triángulo presenta una longitud de hipotenusa que es el doble del tamaño del cateto menor del triángulo De 15 y 75grados El triángulo notable de 15 y 75 es otro clásico que se suele presentar en repetidas ocasiones dentro de los problemas matemáticos De 16 y 74 grados
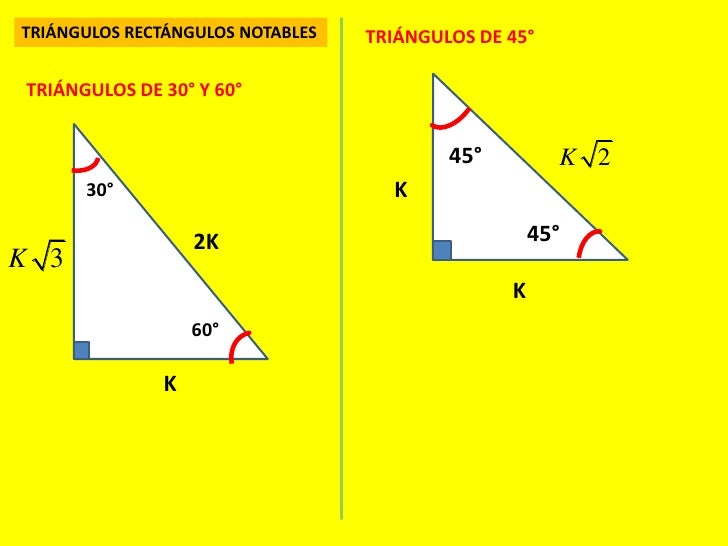
Un triángulo 30°60°90° es comúnmente encontrado como un triángulo rectángulo cuyos lados están en la proporción Las medidas de los lados son x , , y 2 x En un triángulo 30°60°90°, la longitud de la hipotenusa es dos veces la longitud del cateto más corto, y la longitud del cateto más largo es veces la longitud del catetoEl triángulo 45°45°90° es un triángulo rectángulo cuyos lados se encuentran comúnmente en la proporción Las medidas de los lados son x , x , y En un triángulo 45°45°90°, la longitud de la hipotenusa es por la longitud de un cateto Para ver porque es esto, dese cuenta que por el inverso del teorema de Pitágoras , estos #matemáticas #Triángulo #notable #75°y15° Con este video espero que te ayude a comprender este tema, cualquier duda en dejamelos en los comentarios
Triángulo notable de 15° y 75° Podemos caracterizar a un triángulo como notable cuando existe una relación conocida entre sus lados En la mayoría de los casos, las relaciones entre sus lados se limitan a número enteros o númeroPrimer Triangulo Notable de 30° y 60° con el cable mas corto 3 Segundo Triangulo Notable con 30° y 60° con el cable mas largo Y 2 = 2 a 2 8 2 Y= √ 256 3 Y 2 = 4 (4 √ 3 3) 64 Y = 16 √ 3 3 16 x 3 9 Y 2 = 4 ¿) 64 Y=9237ADMISIÓN 112 CON GRUENCIA DE TRIÁNGULOS




Triangulo Notable De 15 Y 75 6 Youtube



Triangulo Rectangulo
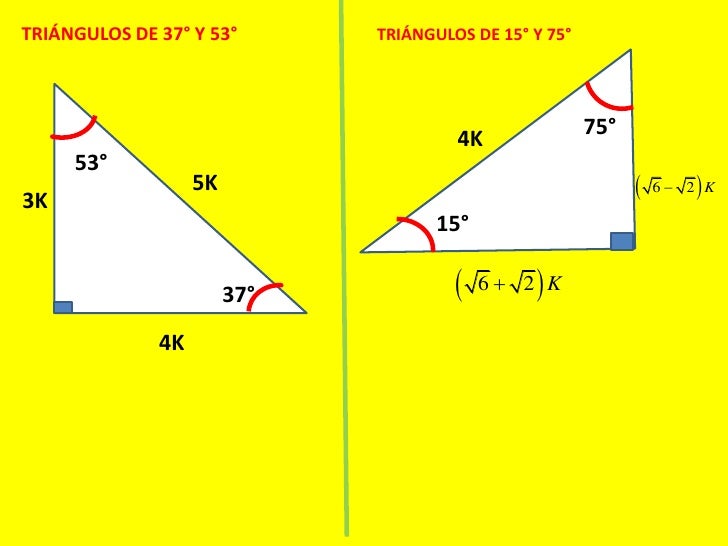
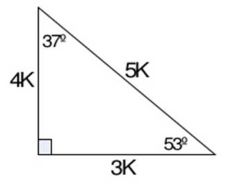
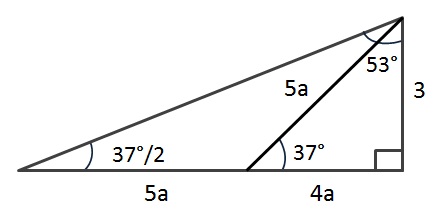
Triángulo de 8 y grados Notable de 36 y 54 grados Triángulo de 18 y 72 grados Triangulo de 15 y 75 grados Triángulo notable de 37/2 grados Triángulo notable de 53/2 grados Razones trigonométricas Las razones trigonométricas de un ángulo agudo, se refiere a la relación que existe entre los lados de un triángulo respecto a un ángulo5 3 4 53° 37° 37° y 53° 3k 4k 53° 37° en particular en general triangulos rectangulos notables 15° y 75° 𝟔 − 𝟐 𝟔 𝟐 75° 15° ( 𝟔 − 𝟐)k ( 𝟔 𝟐)k 75° 15° 1004 pm 6A) incentro b) circuncentro c) ortocentro d) punto de




Triangulos Notables De 15




Resolucion De Triangulos Superprof
Respuesta heart 1 SKing18 el seno del triángulo notable 30 60 es cateto adyacente / hipotenusa en este caso 1/2 y el seno es opuesto / hipotenusa enTriángulo rectángulo de 15 y 75 grados, ayuda como lo resuelvo anyelo está esperando tu ayuda Añade tu respuesta y gana puntos Nuevas preguntas de Matemáticas busco nov1a de 13 años doy coronita znoniduvygdyvudbycydguvdLos principales triángulos notables son A El triángulo notable de 45° y 45° F Triángulo de 36° y 54° G Triángulo de 8° y ° B El triángulo de 30° y 60° H Triángulo de 16° y 74° C El triángulo de 37° y 53° I Triángulo de 37°/2 D Ei triángulo de 15° y 75° J Triángulo de 53°/2




Triangulo Notable De 15º Y 75º Demostracion Youtube



Triangulos Notables
Lo bueno, malo y feo de la capacitación a directores Jesus Mendez Leer Teoría Triángulo Notable de 15° y 75° previous Razones trigonométricas de ángulos notables Parte II next Triángulo Notable de 37°/2 y 53°/2 teniendo en cuenta sus propiedades y proporciones resolveremos problemas respecto a este triangulo notableOsea el 8% y Cuanto debe pagar el cliente?




Los Triangulos Rectangulos Notables Y Sus Respectivos Angulos



Q Tbn And9gcsrwu7na8r5qsqei39hph1wf7g6vpc rb Tgmzjwfsp1hrf5n Usqp Cau
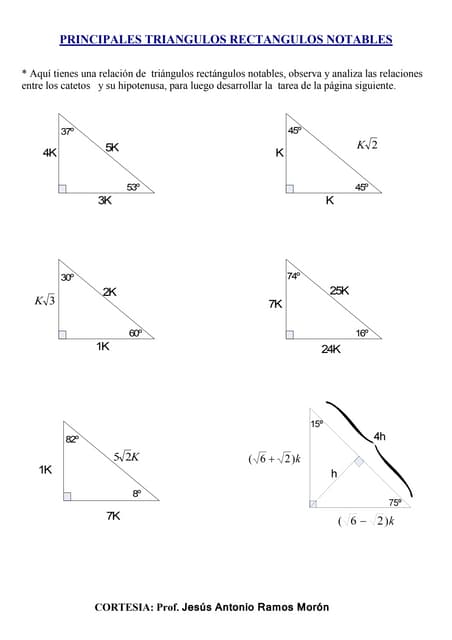
En los triángulo notable existe una relación conocida entre sus lados y ángulos Los triángulos notables son de 37°, 53°, 45°, 74°,76°, 30°, 60° entre otros Triangulos rectangulos notables (completo) 1 TRIÁNGULOS RECTÁNGULOS NOTABLES 2k k 3k 30° 60° 5k 3k 4k 37° 53° 2k k k 45° 45° 25k 7k 24k 16° 74° 17k k 4k 14° 76° 4k ( 6 2)k 15° 75° 10k k 3k 37 2 ° 5k k 2k 5 2k k 7k 8° ° 137k 11k 4k 70° ° 61k 6k 5k 50° 40° 4k ( 5 1)k ( )10 2 5k 18° 72° 4k ( )10 2 5k ( )5 1k 36Se denomina triángulo notable a todo triángulo cuyos lados sean conocidos En




Geometria Triangulos Ii Brainly Lat




Pin En Libro Logica
No hay triangulo notable con esos catetos, pero "a" vale 2√13 solo haces pitagoras y cuanto se ahorra? Triángulo Notable de 15° y 75° next Triángulo Notable de 37°/2 y 53°/2 Jesus Mendez Entradas Relacionadas Números Reales, Naturales, Enteros, Racionales e Irracionales Jesus Mendez 0 Razones trigonométricas inversas o reciprocas y complementariasH = √ a^2 b^2 ¿Qué dice el teorema de Pitágoras?



Triangulos Notables By Nicolas Medina By Nicolasmed0123 On Emaze



Es Static Z Dn Net Files D15 4da1bb799feaa7a35cfc248 Pdf
Triángulo notable de 54° y 36° Razones trigonométricas de los triángulos notables Triángulo notable de 75° y 15° Otros Triángulos Notables ¿Qué es un triangulo notable?TRIÁNGULOS NOTABLES EJERCICIOS RESUELTOS PDF Demostración del Triangulo de 30° y 60° Considerando un triángulo equilátero cuyo lado mide "2a", se traza la altura que también es mediana y bisectriz, entonces por Pitágoras En el BHC (30° y 60°) el cateto adyacente a 60° mide la mitad de la hipotenusaPublishing platform for digital magazines, interactive publications and online catalogs Convert documents to beautiful publications and share them worldwide Title TRIÁNGULOS NOTABLES Y POR APROXIMACIÓN, Author JUSTO GUSTAVO INGA FLORES, Length 2




Triangulos Rectangulos Notables Matemath Web




Tu Bloc De Notas Triangulos Notables
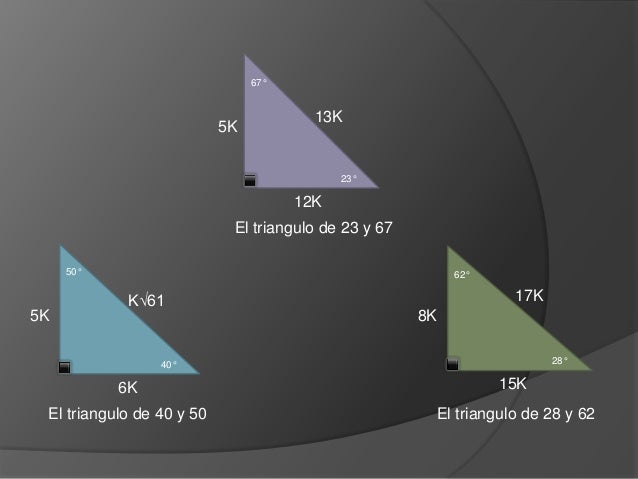
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us CreatorsOtros triangulos notables Otros triángulos notables no tan conocidos son El triángulo de 15 y 75 El triángulo de 18 y 72 El triángulo de 36 y 54 Publicado por Unknown en 1309 Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Etiquetas Otros triangulos notables Entrada ° 1K K√50 8° 7K El triangulo de 8 y 30° K √3 74° 2K 25K 7K 60° 1K El triangulo de 30 y 60 16° 24K El triangulo de 16 y 74 8 √10K K 37°/2 3K El triangulo de 37/2 75° (√6 √2)K 4K √5 K K 15° (√6 √2)K El triangulo de 15 y 75 53°/2 2K El triangulo de 53/2 9




Todo Los Triangulos Notables Sus Angulos Medidas




Todo Los Triangulos Notables Sus Angulos Medidas
2 1era aplicación del triángulo notable de 37° y 53° 3k = a m 2 = 3 2 4 2 3(1) = a m 2 = 9 16 3 = a m 2 = 25 m = √ 25 m = 5m 3 2da aplicación del triángulo notable de 37° y 53° n 2 = 6 2 8 2 n 2 = 36 64 n 2 = 100 n = √ 100 n = 10m 1 torre 5m 10m cantidad total = 15 x 125 1 torre 15m cantidad total = 1 875m 125 125 125K El triangulo notable de 45 y 45 53 3K El triangulo de 37 y 53 1K K50 7K El triangulo de 8 y 30 K 3 74 2K 25K 7K 16 60 1K El triangulo de 30 y 60 24K El triangulo de 16 y 74 10K 37/2 3K El triangulo de 37/2 75 4K 5 K (6 2)K K 15 53/2 (6 2)K 2K El triangulo de 15 y 75 El triangulo de 53/2 67 5K 13K 23Triángulo notable de 45°Triángulo notable de 37° y 53°De 30° y 60°De 15° y 75° ¿Cuáles son las funciones trigonométricas?



Deducciones Del Teorema De Pitagoras A Lo Largo De La Historia Como Recurso Didactico En El Proceso De Ensenanza Aprendizaje De La Matematica



2 Supongamos Que Tenemos Una See How To Solve It At Qanda
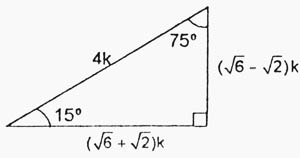
Los más conocidos son de 45°, 37° y 53°, 60° y 30°, 15° y 75°, 74° y 16° pero los triángulos notables más usados son 45°, 37° y 53°, 60° y 30° (grados sexagesimales Elementos de un triángulo Antes de conocer los triángulos notables repasemos un poco de lo que son los elementos del triánguloDe 15 y 75grados El triángulo notable de 15 y 75 es otro clásico que se suele presentar en repetidas ocasiones dentro de los problemas matemáticos De 16 y 74 grados Este triángulo notable es bastante sencillo de aprender por las proporciones enteras que posee• Ahora calculo la longitud de la rampa cuando el ángulo es de 15° 1 representación gráfica de la rampa 2 triángulo notable de 15 y 75° Relaciono las longitudes de los lados de ambos triángulos En 2, calculo el valor de la constante k Calculo la longitud x de la rampa x = 4k x = 4(1,44 m) x = 5,76 m 1,5 m = k( 6– 2) 15° 15




Todo Los Triangulos Notables Sus Angulos Medidas



Un Triangulo Rectangulo Tiene Angulos Agudos A Y B Si Y
Seno, coseno, tangente, cotangente, secante y cosecante ¿Cómo se halla la hipotenusa? Respuesta Triangulos notables Rpta6 y 6 raiz de 3 Explicación paso a paso El triangulo notable es el siguiente 30=K 60=k y 90=2k Reemplazando k vale 6 Bagg Para ambos caso el triangulo notables es el triangulo recto Debemos recordar que un triangulo recto o rectángulo es aquel que tiene un angulo de 90° Así mismo, la suma de todos los ángulos internos de un triangulo debe sumar 180° En el primer caso, tenemos los angulo 10 y 80, por lo tanto 10 80 x = 180 x = 180 90




Triangulos Notables Estudiandoenlinea




Triangulo Rectangulo Problema 7 Basico
Triángulo notable de 15° y 75° Podemos caracterizar a un triángulo como notable cuando existe una relación conocida entre sus lados En la mayoría de los casos, las relaciones entre sus lados se limitan a número enteros o número Ejemplo Hallar la hipotenusa del siguiente triangulo sabiendo que el ángulo que se le antepone al ángulo de 37° es 9 Explicación Triangulo Notable El cateto mas pequeño es aquel que se opone al ángulo mas pequeño y así viceversa Son aquellos triángulos que a partir de la razón Triángulo notable de 15° y 75° Podemos caracterizar a un triángulo como notable cuando existe una relación conocida entre sus lados En la mayoría de los casos, las relaciones entre sus lados se limitan a número enteros o número TRIÁNGULOS RECTÁNGULOS NOTABLES DE 30°, 60°, 45°, 37°, 53°
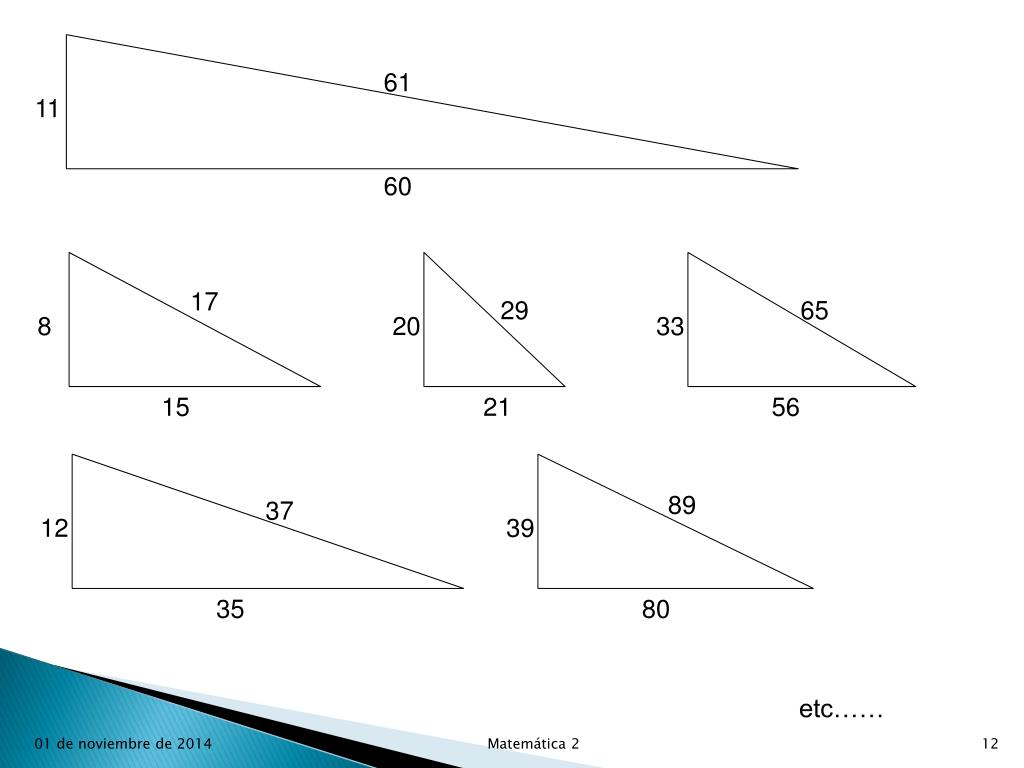



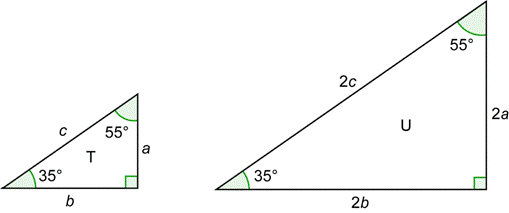
Ppt Matematica 2 Epe Powerpoint Presentation Free Download Id




Todo Los Triangulos Notables Sus Angulos Medidas
Los triángulos notables más conocidos son El triangulo notable de 45 y 45 El triangulo de 30 y 60 El triangulo de 37 y 53 El triangulo de 37/2 El triangulo de 53/2 El triangulo de 8 y El triangulo de 16 y 74 Publicado por Unknown en 1424Demostración del Triangulo de 30° y 60° Considerando un triángulo equilátero cuyo lado mide "2a", se traza la altura que Notable (15°–75°) Triángulo Rectángulo Notable (22°30'–67°30') Triángulo Rectángulo




Triangulos Notables
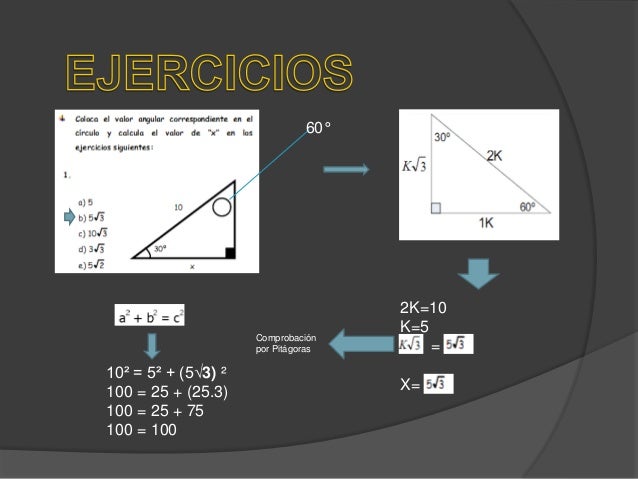



Triangulos Notables
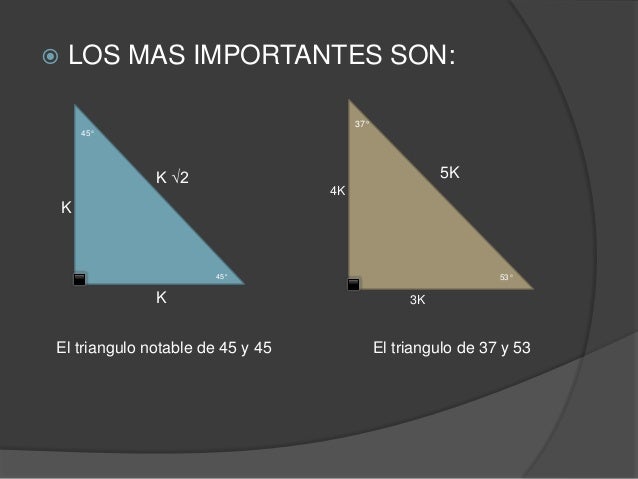



Triangulos Notables



Triangulo Rectangulo



Resources Aprendoencasa Pe Perueduca Secundaria 5 Semana 14 Pdf S14 Sec 5 Solucion Matematica Dia 3 Pdf




Triangulos Notables Wikipedia La Enciclopedia Libre



Triangulos By Romario Kaliman On Emaze




Unidad I Utilicemos Las Razones Trigonometricas Ppt Descargar



Las Razones By Nanogom4 On Emaze



Triangulos Notables Recurso Educativo Tiching



Triangulos Notable Matematica Para Secundaria



Triangulos Rectangulos Notables Completo




Hallar A B Triangulos Notables Brainly Lat
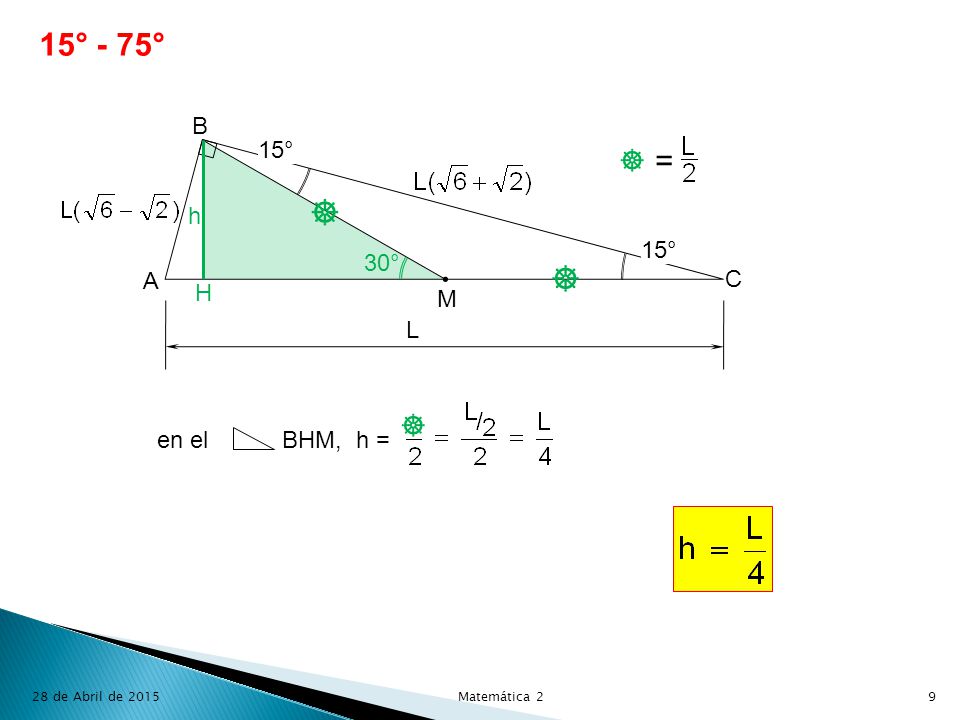



Matematica 2 Epe Area De Ciencias Ma De Abril De Ppt Descargar
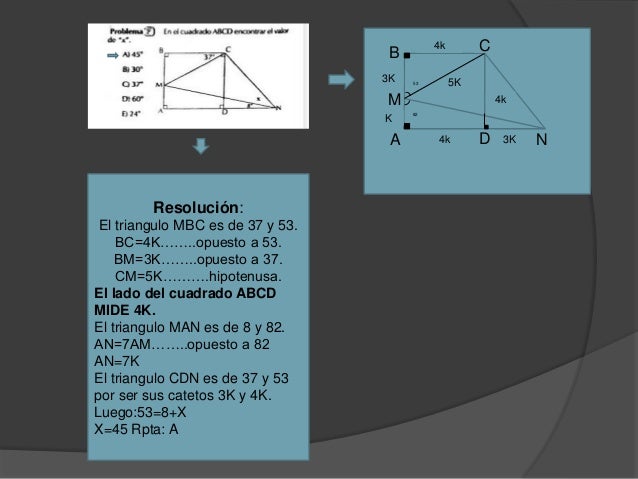



Triangulos Notables




Todo Los Triangulos Notables Sus Angulos Medidas
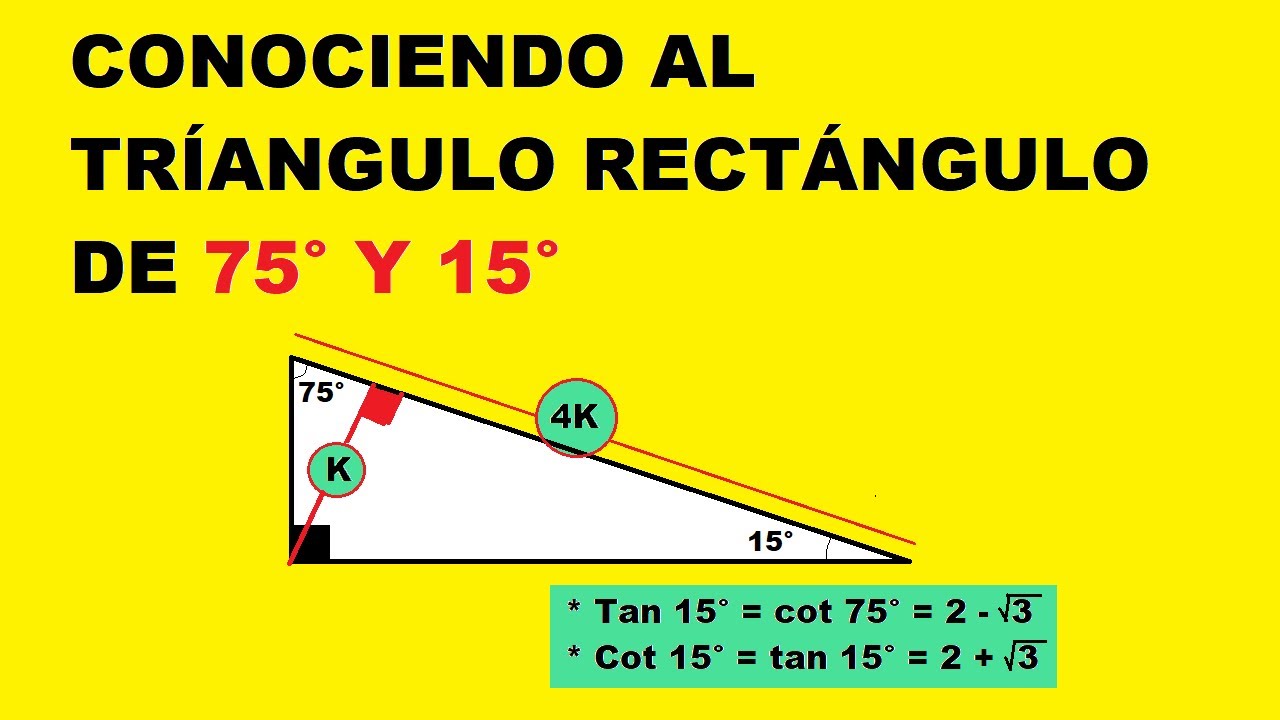



Un Interesante Triangulo Notable 75 Y 15 Conclusiones Youtube



1
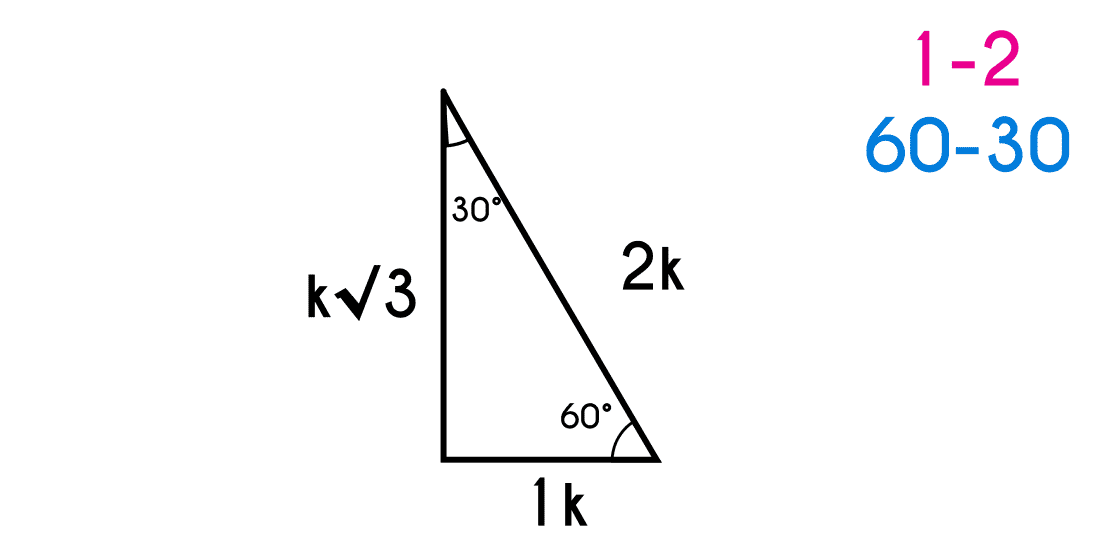



Triangulos Notables Fhybea
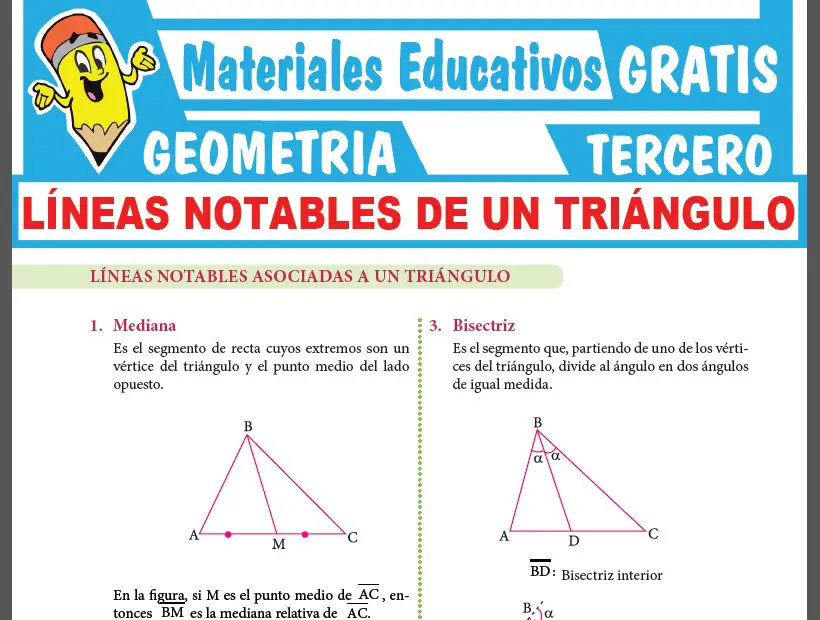



Triangulos Rectangulos Notables Y Pitagoricos Para Tercer Grado




Resolucion De Triangulos Superprof




Todo Los Triangulos Notables Sus Angulos Medidas
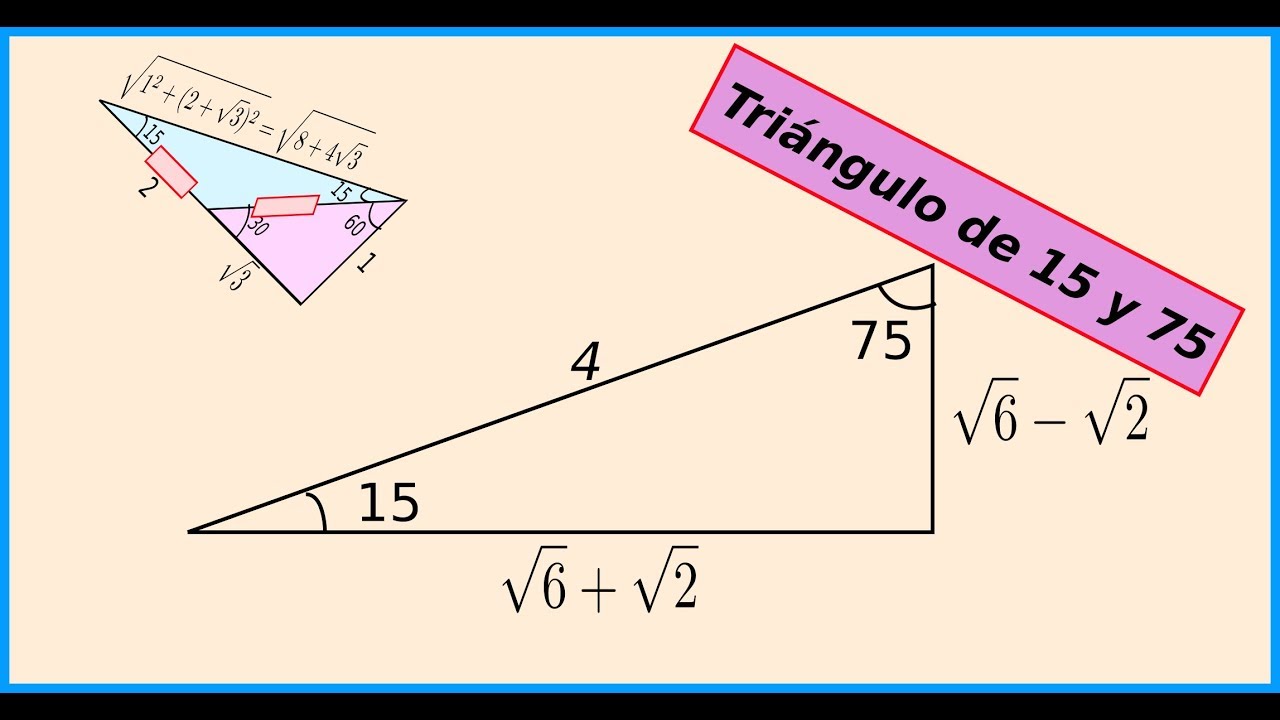



El Triangulo De 15 Y 75 Grados Youtube




Triangulo Rectangulo Notable De 15 Y 75 Youtube




Todo Los Triangulos Notables Sus Angulos Medidas




Triangulos Notables Reto Y Ejercicios Propuestos Matemovil



Edoc Pub Download Triang Ulos Notables Pdf Free Html




Congruencia De Triangulos Profesor De Matematica Facebook
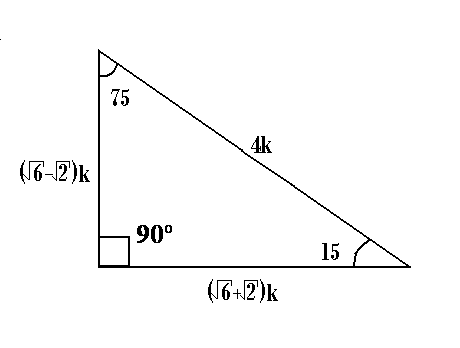



File Triangulo Auxiliar De 75 Y 15 Png Wikimedia Commons




Triangulos Rectangulos Notables Matemath Web




Triangulos De 30 Y 60 45 Y 45 37 Y 53 Razones Trigonometricas Notables Ejercicios Res Razones Trigonometricas Ejercicios Resueltos Formulas Matematicas




Triangulo Notable De 45º




Triangulo Rectangulo




Los Triangulos Rectangulos Notables Y Sus Respectivos Angulos
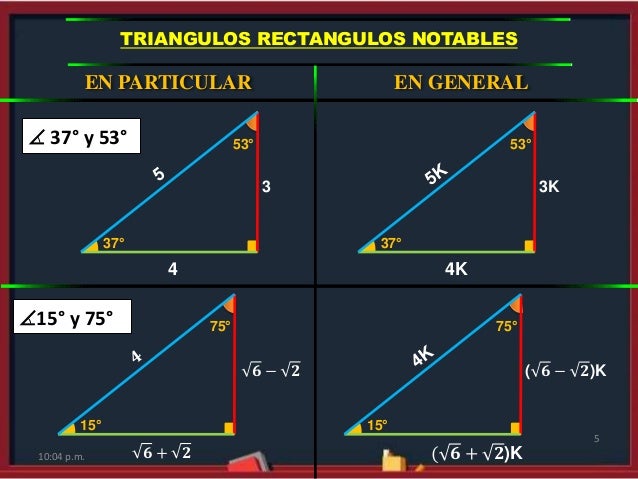



Triangulos Rectangulos Notables




Pin En Problemas



Http Www Itsmante Edu Mx Wp Content Uploads 17 11 Cuadernillo De Trigonometria Pdf




Triangulos Rectangulos Notables Matemath Web




Triangulos Notables
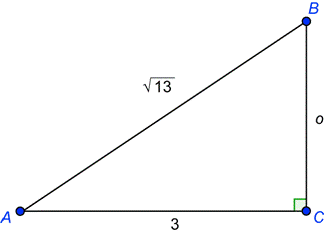



Un Triangulo Rectangulo Tiene Angulos Agudos A Y B Si Y




Triangulos Notables Ejercicios Resueltos Pdf




Todo Los Triangulos Notables Sus Angulos Medidas
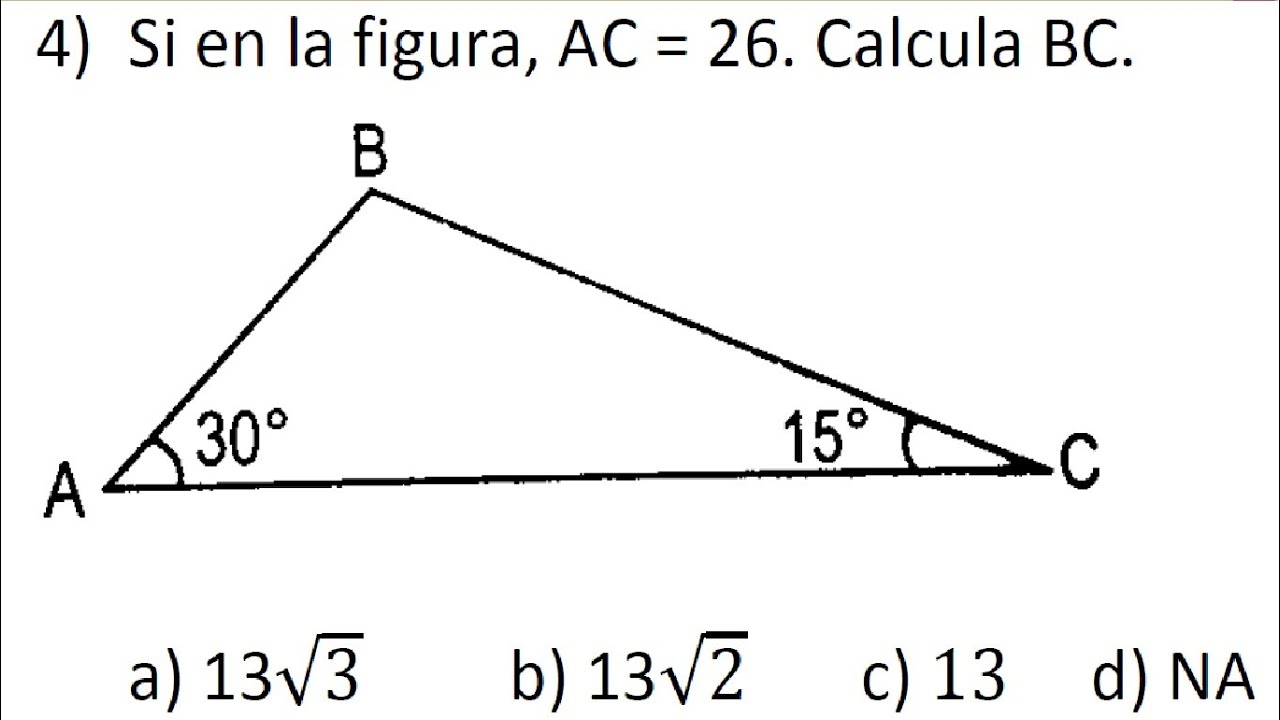



Triangulo Rectangulo Notable 15 Y 75 Youtube




Resolucion De Triangulos Superprof




Puntos Y Rectas Notables Del Triangulo Matematicascercanas




Todo Los Triangulos Notables Sus Angulos Medidas




Todo Los Triangulos Notables Sus Angulos Medidas
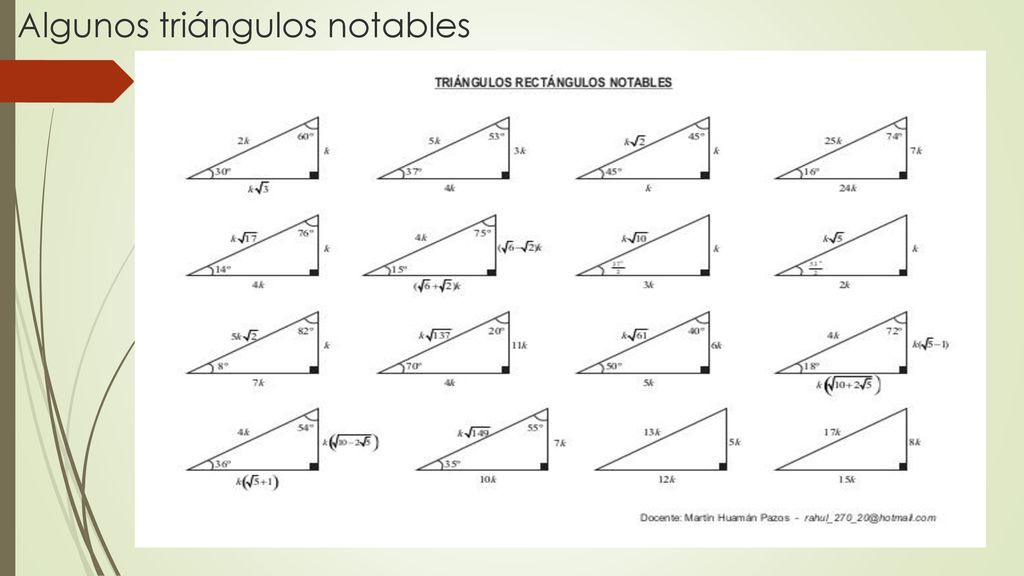



Razones Trigonometricas En El Triangulo Rectangulo Ppt Descargar




Triangulos Rectangulos Notables Completo




Todo Los Triangulos Notables Sus Angulos Medidas




Triangulos Rectangulos Notables Matemath Web




Triangulos Rectangulos Notables Matemath Web




Triangulo Notable De 15 Y 75 Profesorajesus Com



Aekngjyixh2wrm




Todo Los Triangulos Notables Sus Angulos Medidas
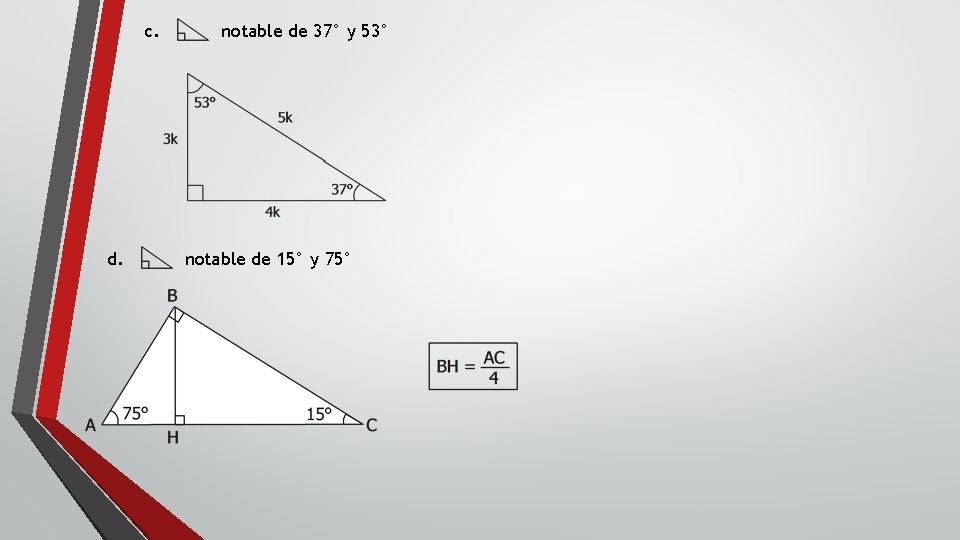



Triangulos Notables 15 75




Todo Los Triangulos Notables Sus Angulos Medidas




Triangulos Rectangulos Notables Matemath Web




Todo Los Triangulos Notables Sus Angulos Medidas




Triangulo Rectangulo Notable De 15 Y 75 Youtube




El Cerebrito Importantes Triangulos Rectangulos Notables Facebook
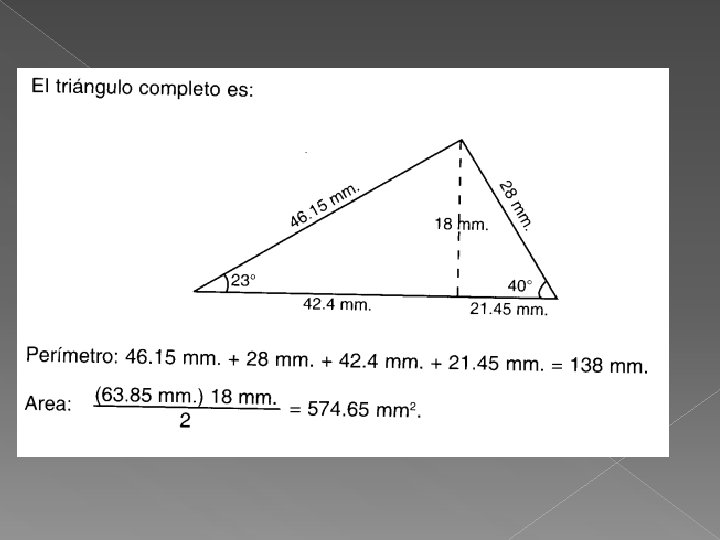



Unidad I Utilicemos Las Razones Trigonometricas Trigonometra Es



Resources Aprendoencasa Pe Perueduca Secundaria 5 Semana 14 Pdf S14 Sec 5 Solucion Matematica Dia 3 Pdf




Triangulos Rectangulos Notables Completo




Todo Los Triangulos Notables Sus Angulos Medidas
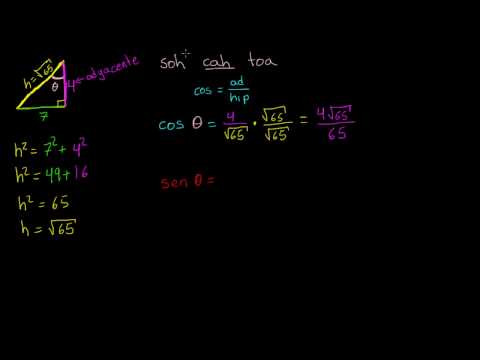



Razones Trigonometricas En Triangulos Rectangulos Video Khan Academy



1



Triangulos Notables Reto Y Ejercicios Propuestos Matemovil




Triangulo Rectangulo De 75 Y 15 Youtube




Todo Los Triangulos Notables Sus Angulos Medidas




Triangulos Rectangulos Notables Matemath Web



Http Www Itsmante Edu Mx Wp Content Uploads 17 11 Cuadernillo De Trigonometria Pdf



Http Www Itsmante Edu Mx Wp Content Uploads 17 11 Cuadernillo De Trigonometria Pdf




Ejercicios Con Triangulos Oblicuangulos Superprof
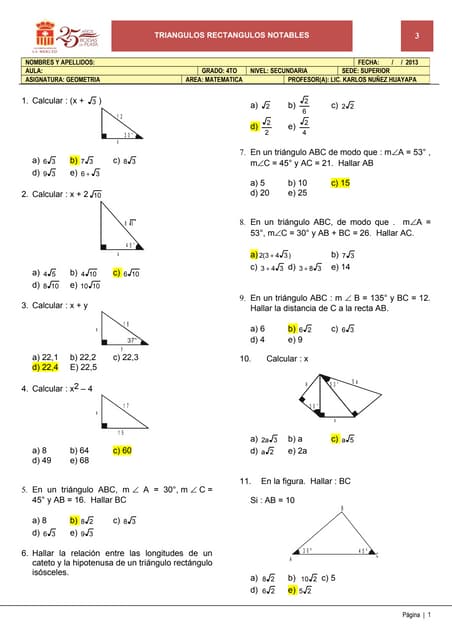



Triangulos Notables
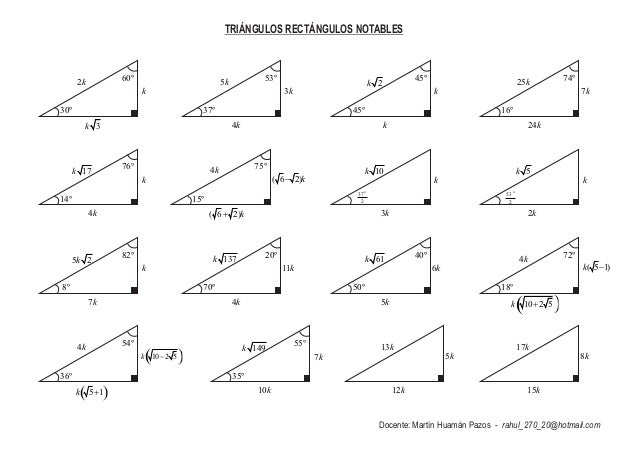



Triangulos Rectangulos Notables Completo




Ejercicios De Triangulos Notables Ayudenme A Resolver Estos Ejercicios Xfa Brainly Lat




Triangulos Rectangulos Notables



1




Math Periodic Table Education



0 件のコメント:
コメントを投稿