= P 2 d Q R (Q2 PR)Vdz is a binomial unit > 1 and this is impossible This completes the proof7 4(p – q) (4 p 3q) = 16 p2 – 4pq – 12q 2 8 7(x 3 y) (5 x – 2y) = 35 x2 91 xy – 42 y2 Factorisation Worksheet 1 Take out the common factors from each of the following 1 qt rt = t(q r) 2 rt – 5rs = r(t – 5s) 3 3xy 4 xz = x(3 y 4z) Using difference of two squares factorise the following 4 p2 q2 = (p q)(p (v) p 3 q 6 − p 6 q 3 = p 3 q 3 (q 3 − p 3) (p 3 q 6 – p 6 q 3) ÷ p 3 q 3 = p 3 q 3 q 3 – p 3 p 3 q 3 = q 3 – p 3 P3 Work out the following divisions (i) (10x − 25) ÷ 5 (ii) (10x − 25) ÷ (2x − 5) (iii) 10y(6y 21) ÷ 5(2y 7) (iv) 9x 2 y 2 (3z − 24) ÷ 27xy(z −
2
Factorise (p+q)^2-20(p+q)-125
Factorise (p+q)^2-20(p+q)-125-Factorising quadratic expression of the forms px 2 q where p and q are perfect square Use the identity a 2 b 2 = ( a b )( a b ) , the difference between two squares Example$\endgroup$ – Mark Bennet Oct 2 ' at 1139



2
Mathematics NCERT Grade 8, Chapter 14 Factorisation The chapter lays emphasis on the concept of how to express algebraic expressions as the products of their factors In the introduction part following topics are discussed 1 Factors of natural numbers 2 Factors of algebraic expressionsThe Factor Theorem states that if P/Q is root of a polynomial then this polynomial can be divided by q*xp Note that q and p originate from P/Q reduced to its lowest terms In our case this means that 3x 3x 2x12 can be divided by 3 different polynomials,including by x3 Polynomial Long Division 24 Polynomial Long Division Important Questions for Class 10 Maths Chapter 8 Introduction to Trigonometry Introduction to Trigonometry Class 10 Important Questions Very Short Answer (1 Mark) Question 1 If tan θ cot θ = 5, find the value of tan2θ cotθ (12)
P = 4 Supplement Solving Quadratic Equation Directly Solving p 2 p = 0 directly Earlier we factored this polynomial by splitting the middle term let us now solve the equation by Completing The Square and by using the Quadratic Formula Parabola, Finding the Vertex 31 Find the Vertex of y = p 2 p3 1 –1 p 24 3 6 18 3 p 1 2 6 p 42 3 p Since 3 x = is a root, the remainder is zero 42 3 0 3 42 14 p p p = = = Note This is just the same synthetic division procedure we are used to Higher Mathematics Unit 2 – Polynomials and Quadratics Page HSN0 hsn uknet 2Solution Steps { x }^ { 3 } 3 { x }^ { 2 } 4 = 0 x 3 − 3 x 2 4 = 0 By Rational Root Theorem, all rational roots of a polynomial are in the form \frac {p} {q}, where p divides the constant term 4 and q divides the leading coefficient 1 List all candidates \frac {p} {q} By Rational Root Theorem, all rational roots of a polynomial are
Factorise (i) \( 4 p^{2}=9 q^{2} \) (ii) \( 63 a^{2}112 b^{2} \) (iii) \( 49 x^{2}36 \) (iv) \( 16 x^{3}144 x \) (v) \( (lm)^{2}(lm)^{t} \) (vi) \(9 x^{2} y^{210 28 Solve the following equations 4 a) 5 x5− 2x− 1 x2−25= 15 16 b) 2x1 2x1−3 2x−1 6−2x2= 11 26 29 Cost of an adult ticket for the movie is $ 16 and one children ticket costs half of the adult's ticket price a) Calculate the total cost of 197 adult tickets and 22 children tickets Upload your study docs or become aThis is what we shall do now 1421 Method of common factors • We begin with a simple example Factorise 2x 4 We shall write each term as a product of irreducible factors;
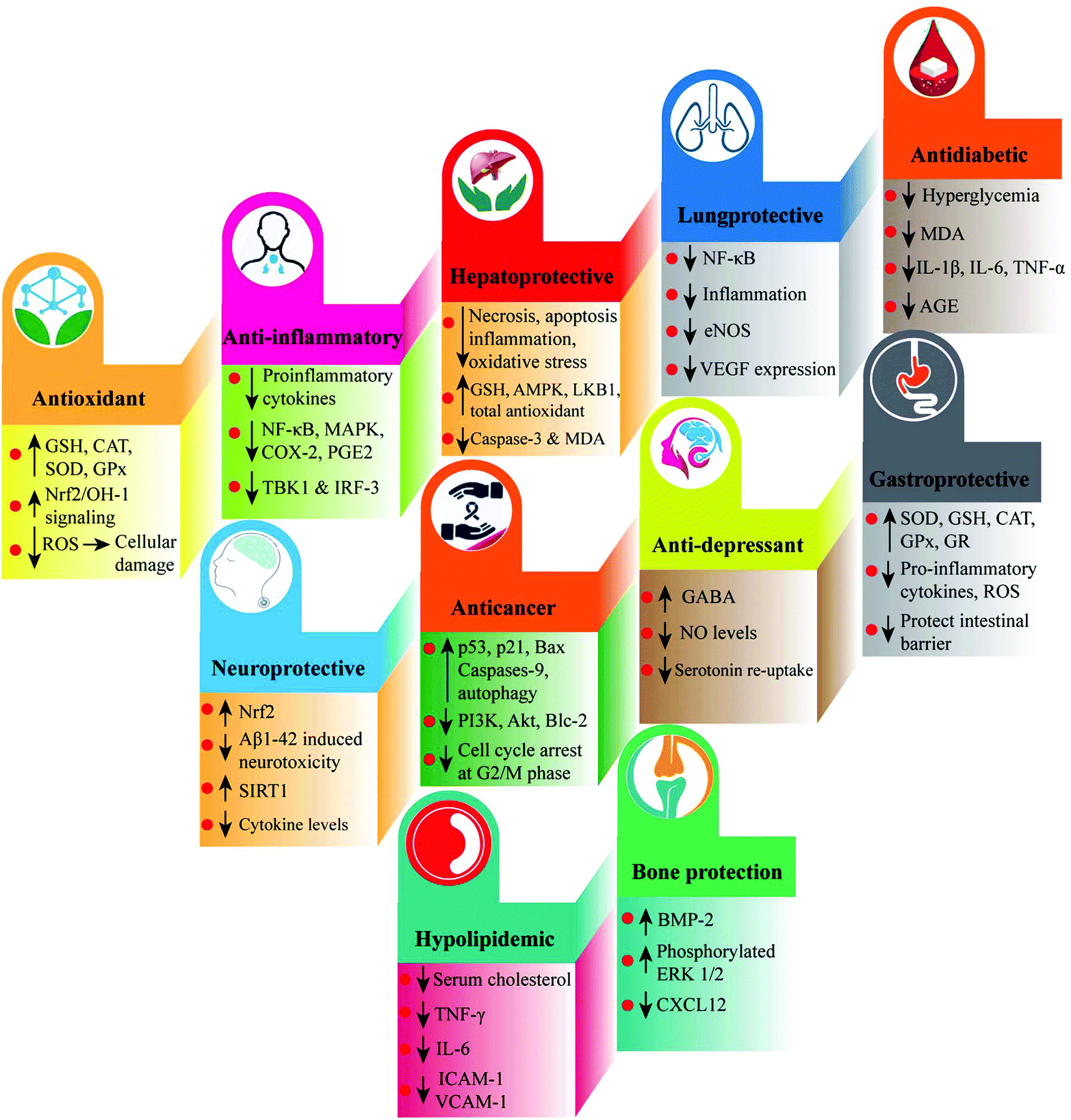



Therapeutic Perspectives Of The Black Cumin Component Thymoquinone A Review Food Function Rsc Publishing



Factorize 6i P Q 2 P Q 125 Brainly In
Exercise 141 Question 1 Find the common factors of the terms (i) 12 x , 36 (ii) 2 y , 22 xy (iii) 14 pq , 28 p 2 q 2 (iv) $\begingroup$ Look at $(2X3Y)^2$ $\endgroup$ – Damien Oct 2 ' at 1137 2 $\begingroup$ Can you factorise $4x^212x9$?Click here👆to get an answer to your question ️ Factorize x^3 13x^2 32x



2
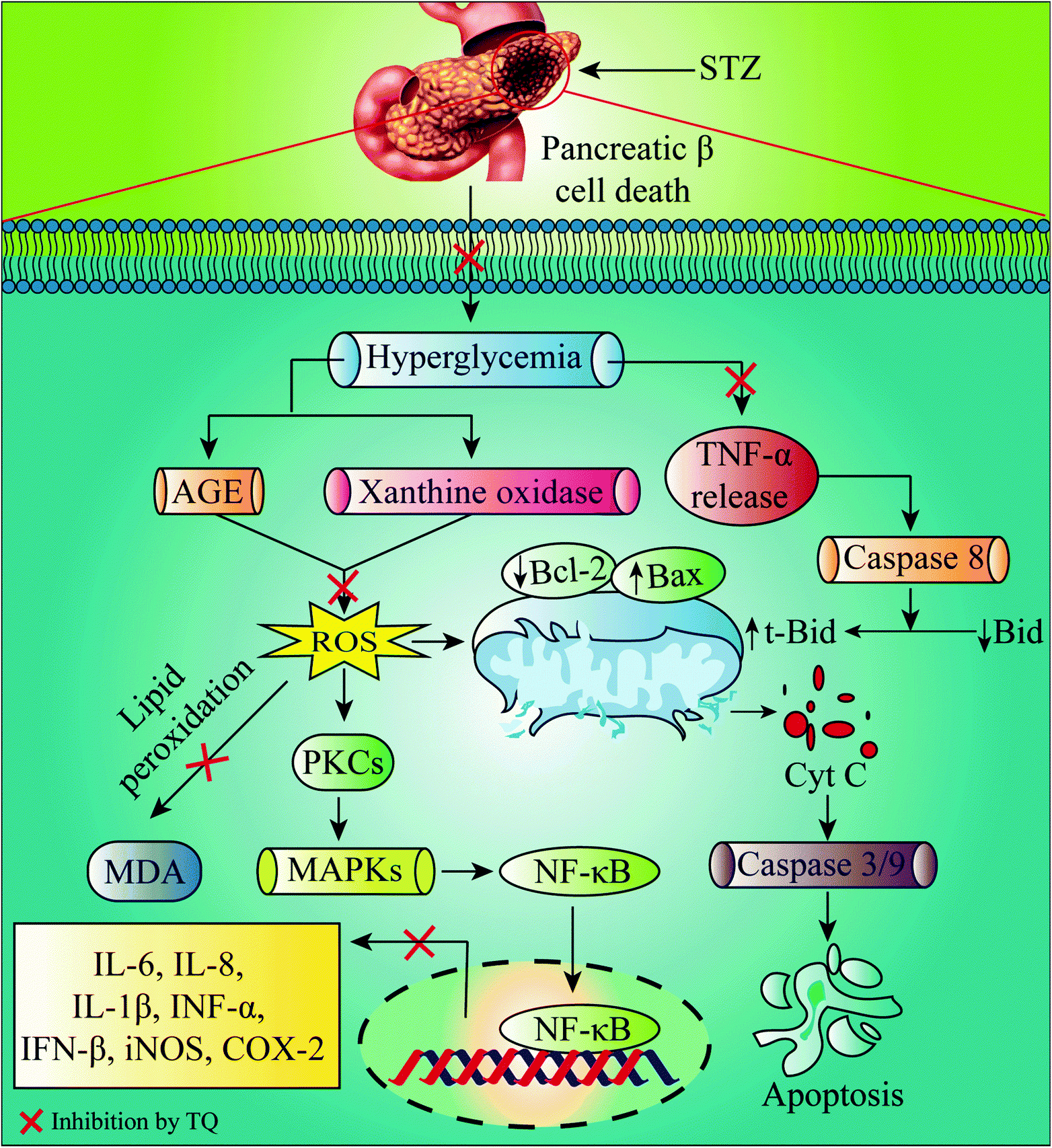



Therapeutic Perspectives Of The Black Cumin Component Thymoquinone A Review Food Function Rsc Publishing
Topic 3 H Simplifying and Substitution St Paul's Catholic School 1 Section A Substitution Grade F / E 1 (a) Find the value of 3x 4y (i) when x = 2 and y = 5 AnswerFor pq=1 it should have value 1 (checked with some trial values), suggesting that some power of (pq) is a factor Is it possible to factorise it in these terms?→ 3130 ( talk ) 2211, January 14 (UTC)2x =2× x 4 =2 × 2 Hence 2x 4 = (2 × x) (2 × 2) Notice that factor 2 is common to both the terms




Enhancing Social Interaction In Depression Side Study Protocol Of A Randomised Controlled Trial On The Effects Of A Cognitively Based Compassion Training Cbct For Couples Bmj Open
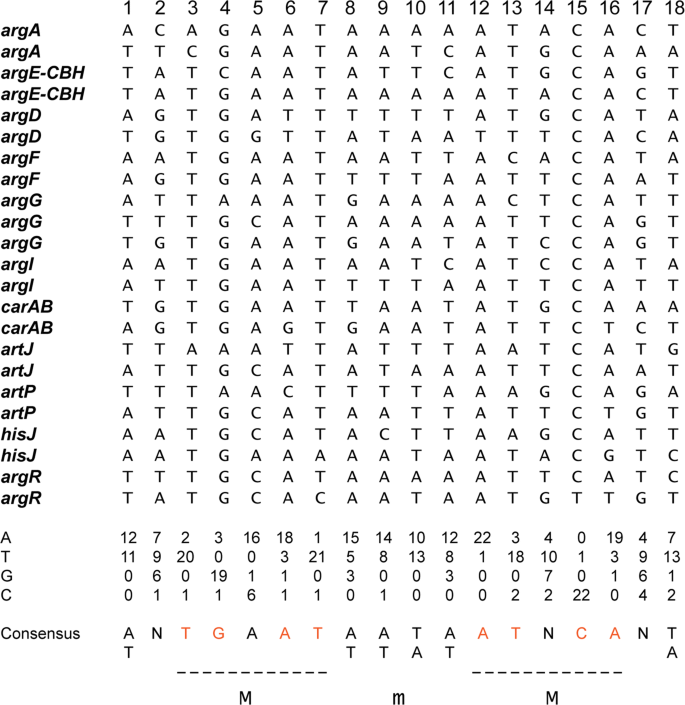



Regulation Of Arginine Biosynthesis Catabolism And Transport In Escherichia Coli Springerlink
(b) p = 5 # 109 q = 9 # 1016 Expressing each answer in standard form, find (i) p # q, Answer 1 (ii) q Answer 1 17 (a) Find 110% of 70 Answer 1 (b) When new, a car was worth $15 000 After one year it was worth $12 000(P^2q^2r^2)^2 4p^2q^2 =(p^2q^2r^2)^2 (2pq)^2 =(p^2q^2r^22pq)(p^2q^2r^2–2pq) =(p^2q^22pqr^2)(p^2q^2–2pqr^2) ={(pq)^2 r^2}{(pq)^2 r^2} =(pqThe common factors are 2, y The common factors are 2, 7, p, q The common factor is 1 12 a2b = 2 × 2 × 3 × a × a × b The common factors are 2, 3, a, b −4 x2 = −1 × 2 × 2 × x × x The common factors are 2, 2, x The common factors are 2, 5 (viii) 3 x2y3 = 3 × x × x × y × y × y




Aga Technical Review On Gastric Intestinal Metaplasia Epidemiology And Risk Factors Gastroenterology



2
Finally, we will see how this can be used to fully factorise a polynomial expression and use the factorised version to sketch the curve Play The final video in the series on polynomials We''ll be looking at factor theorem and how we can use it to help factorise cubic and even quartic (power 4) equations (p=6\) and \(q=14\) \(p=2\) andThe PDF's of this chapter are available here, students can download for free from the links given below Chapter 7 Factorization contains nine exercises and the RD Sharma Solutions present in this page provide solutions for the questions present in each exercise Now, let us have a look at the concepts discussed in this chapter Factorise `(pq)^3(qr)^3(rp)^3` Factorise `(pq)^3(qr)^3(rp)^3` Books Physics NCERT DC Pandey Sunil Batra HC Verma Pradeep Errorless Chemistry NCERT P Bahadur IITJEE Previous Year Narendra Awasthi MS Chauhan 2 If ,




Ix Polynomials Factorise P Q 2 p Q 125 Youtube
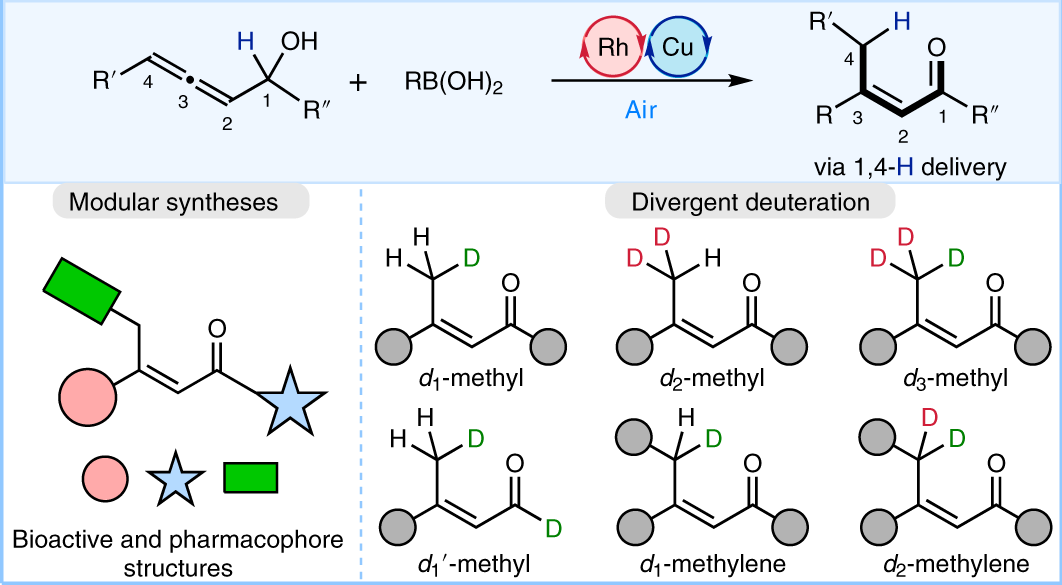



Stereodefined Rhodium Catalysed 1 4 H D Delivery For Modular Syntheses And Deuterium Integration Nature Catalysis
Find the quotient of each of the following a 5mn n 2 d 12 xy 2 4 x 2 yz b 12ab 4ab c 3st ( 12s 2 ) e 3 pqr 9 p 2 q 2 pr d 12 pq 4q 2 p 2 e 10a 2bc 5ab 2c 7Solution Steps 5 { x }^ { 3 } { x }^ { 2 } x4=0 5 x 3 − x 2 − 2 0 x 4 = 0 By Rational Root Theorem, all rational roots of a polynomial are in the form \frac {p} {q}, where p divides the constant term 4 and q divides the leading coefficient 5 List all candidates \frac {p} {q} By Rational Root Theorem, all rational roots of a Factorize p²q – pr² – pq r² Solution Given p²q – pr² – pq r 2 Grouping similar terms together we get = p 2 q – pq – pr 2 r 2 Taking the similar terms common we get = pq (p – 1)r 2 (p – 1) Therefore, as (p – 1) is common = (p – 1) (pq –



Economics Archive April 07 19 Chegg Com




Finding Zeros Of Polynomials 2 Of 2 Video Khan Academy
Perfect Square Trinomials We may check the pattern of the expression to determine whether it is a Perfect Square Trinomial, namely, p 2 2pq q 2 = ( p q )Answer (i) 12x = 2 x 2 x 3 x x 36 = 2 x 2 x 3 x 3 The common factors are 2, 2, 3 And, 2 x 2 x 3 = 12 (ii) 2y = 2 x y 22xy = 2 x 11 x x x y The common factors are 2Thus solving P(x) = 0 is reduced to the simpler problems of solving Q(x) = 0 and R(x) = 0 Conversely, the factor theorem asserts that, if r is a root of P(x) = 0, then P(x) may be factored as = (), where Q(x) is the quotient of Euclidean division of P(x) = 0 by the linear (degree one) factor x – r



Oxidative Stress Induced Formation Of Covalently Linked Ribulose 1 5 Bisphosphate Carboxylase Oxygenase Large Subunit Dimer In Tobacco Plants Bmc Research Notes Full Text




A Parkinson S Disease Circrnas Resource Reveals A Link Between Circslc8a1 And Oxidative Stress Embo Molecular Medicine
(m) 36 d2 (n) 4 q2 (o) 49 w2 (p) x2 64 9 Factorise the following expressions, which contain a difference of squares (a) a2 4b2 (b) x2 25y2 (c) p2 64q2 (d) 16c2 d2 (e) 81 4g2 (f) 36w2 y2 (g) 4a2 1 (h) g2 81h2 (i) 49x2 y2 (j) 9c2 16d2 (k) 4p2 9q2 (l) b2 100c2 (m) 25 16a2 (n) 4d2 121 (o) 225 49k2 (p) 9x2 0·25 10 Factorise the followingAccording to remainder theorem f (2) = 0 so that (x – 2 ) is a factor of x3 2x2 x 2 Here maximum power of x is 3 so that its can have maximum 3 factors So our answer is (x1) (x1) (x2) (ii) x3 3x2 9x 5 Possible zeros are factors of ± constant term / coefficient of leading term Here constant term is 5 and coefficient of Factorise(pq)^3(qr)^3(rp)^3 on studyassistantincom There are 60 boys in a class one boy weighing 50 kg goes away and at the same time another boy joins the classes the average weight of the boys is then increased by 1/4 kg what




Rd Sharma Class 9 Chapter 5 Factorization Of Algebraic Expressions




Prh Represses Transcription In Hematopoietic Cells By At Least Two Independent Mechanisms Sciencedirect
Answer Stepbystep explanationLet p(x) = x3 13x2 32x p(1) = 1 13 32 = 33 33 = 0 Therefore (x 1) is a factor of p(x)Factorise 25k^2(4/k^2) math factorise 15x 6x5y2 Maths how would you factorise this (pq)^25(pq) to get this answer(pq)(pq5) Maths Factorise into quadratics X^24x21 X^24x3 X^29x36 Maths how do you factorise 2xyysqaured?Hence P 3 Q3d 8R3d2 6PQRd = f 1 P 3 Q3d R 3 d 2 3PQRd = 1 9Rd(r2d P Q ) = Hence 0 = a Then either R = 0 and P Q V ~ i i s binomial unit and so n possibility from Lemma 2, or R2d PQ = 0 Then 1 is the only I/?




Doppler Radar Analysis Of The Northfield Texas Tornado Of 25 May 1994 In Monthly Weather Review Volume 125 Issue 2 1997




Performance Of Prp Associated With Porous Chitosan As A Composite Scaffold For Regenerative Medicine
P^3 9q^3(pq) ^3= =2p^3 10q^3–3p^2*q3p*q^2= =(2pb*q)(p^2cq^2dpq)= =2p^32d*p^2*q2cp*q^2bc*q^3bp^2*qbd*p*q^2 =2p^3(2db)*p^2*q(2cbd)p*q^2bc*q^3 So The first step of factorizing an expression is to take out any common factors which the terms have We consider the algebraic expression 4x8 This expression is already simplified but notice that 4 and 8 have a common factor In fact the HCF of 4 and 8 is 4 Now, 8 = 4 x 2 and 4 = 4 x 1 So, 4x 8 = 4 x 1x – 4 x 2 = 4 (x 2) Factorise the following expressions (i) 7x − 42 (ii) 6p − 12q (iii) 7a 2 14a (iv) −16z z 3 (v) l 2 m 30 alm (vi) 5x 2 y − 15xy 2 (vii) 10a 2 − 15b 2 c 2 (viii) −4a 2 4ab − 4 ca (ix) x 2 yz xy 2 z xyz 2 (x) ax 2 y bxy 2 cxyz




Jnk Foxo Mediated Neuronal Expression Of Fly Homologue Of Peroxiredoxin Ii Reduces Oxidative Stress And Extends Life Span Journal Of Biological Chemistry




Math Physics Chemistry Questions Discussion Lists Dated 16 10 02
(iii) 14pq, 28p 2 q 2 Factors of 14pq, 28p 2 q 2 ⇒ 14pq = 2 × 7 × p × q ⇒ 28p 2 q 2 = 2 × 2 × 7 × p × p × q × q So, common factors are ⇒ 2 × 7 × p × q = 14pq (iv) 2x, 3x 2, 4 Factors of 2x, 3x 2, 4 ⇒ 2x = 2 × x ⇒ 3x 2 = 3 × x × x ⇒ 4 = 2 × 2 So, common factor is 1 (∵ 1 is a factor of every number) (v) 6abc, 24ab Class 10 Maths MCQs Chapter 5 Arithmetic Progressions 1 The n th term of an AP is given by a n = 3 4n The common difference is 2 If p, q, r and s are in AP then r – q is 3 If the sum of three numbers in an AP is 9 and their product is 24, then numbers are Also (a – d)ML Aggarwal Solutions PDF of this chapter can be downloaded from the link provided below and can be used for any future references Chapter 10 Algebraic Expressions and Identities contains five exercises and Check your progress questions The ML Aggarwal Class 8 Solutions present on this page provides clear solutions, according to the latest




Jnk Foxo Mediated Neuronal Expression Of Fly Homologue Of Peroxiredoxin Ii Reduces Oxidative Stress And Extends Life Span Journal Of Biological Chemistry



2
12 p is inversely proportional to the square of (q 4) p = 2 when q = 2 Find the value of p when q = –2 Answer p = 3 _____ 13 A car travels a distance of 1280 metres at an average speed of 64 kilometres per hourIn general, it is true that every polynomial splits (ie, factors into linear factors) over the complex number field However, finding this factorization for polynomials of degree up to four is manageable, and factoring something of degree higher than 4 is impossible (in the sense that there does not exist, for a general polynomial of degree 5 or higher, an algorithm for finding its roots) x^39x^224x = (x2)(x2)(x5) f(x) = x^39x^224x By the rational root theorem, any rational zeros of f(x) are expressible in the form p/q for integers p, q with p a divisor of the constant term and q a divisor of the coefficient 1 of the leading term



2



Dynamic Thylakoid Stacking And State Transitions Work Synergistically To Avoid Acceptor Side Limitation Of Photosystem I Nature Plants
Factorise fully3xsquared y9xysquared12xcubed y cubed Maths Factorise as far as possible 1) 2a^2b 8a^2b^2 The answer i got for this is 2ab(a4ab) I'm not entirely sure if this is fully factorised or not Can you please correct me if i am wrong 2) x^2 5x



Bioactive Poly Ethylene Glycol Acrylate Hydrogels For Regenerative Engineering Springerlink
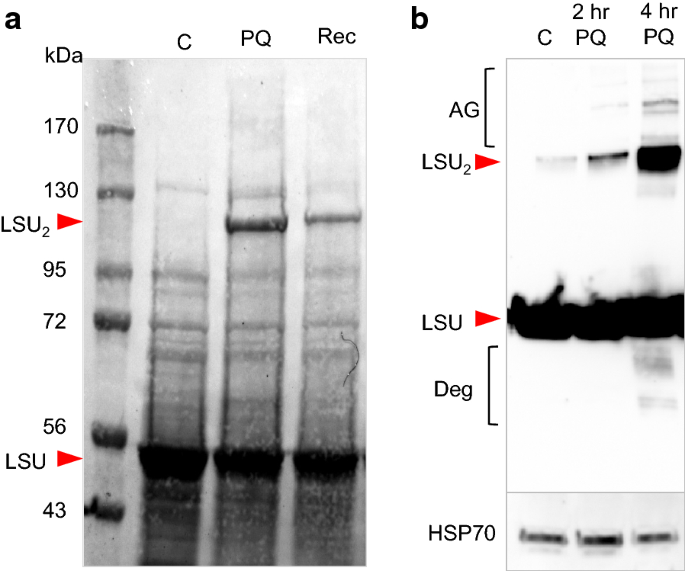



Oxidative Stress Induced Formation Of Covalently Linked Ribulose 1 5 Bisphosphate Carboxylase Oxygenase Large Subunit Dimer In Tobacco Plants Bmc Research Notes Full Text




Olympiad Total Gadha
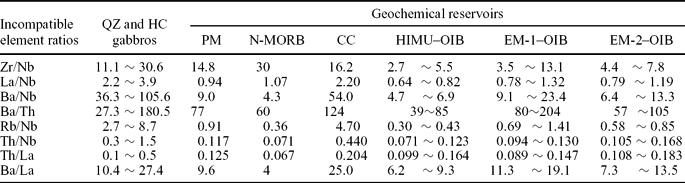



Geochronological Geochemical And Sr Nd Hf Isotopic Constraints On Petrogenesis Of Late Mesozoic Gabbro Granite Complexes On The Southeast Coast Of Fujian South China Insights Into A Depleted Mantle Source Region And Crust Mantle Interactions



2



2




Question 4 Page 15 It Is Required To 125 Marks Design A Cold Storage For Storing Homeworklib



Papers Past Parliamentary Papers Appendix To The Journals Of The House Of Representatives 1925 Session I Public Works Statement By The Hon J G Coates



2
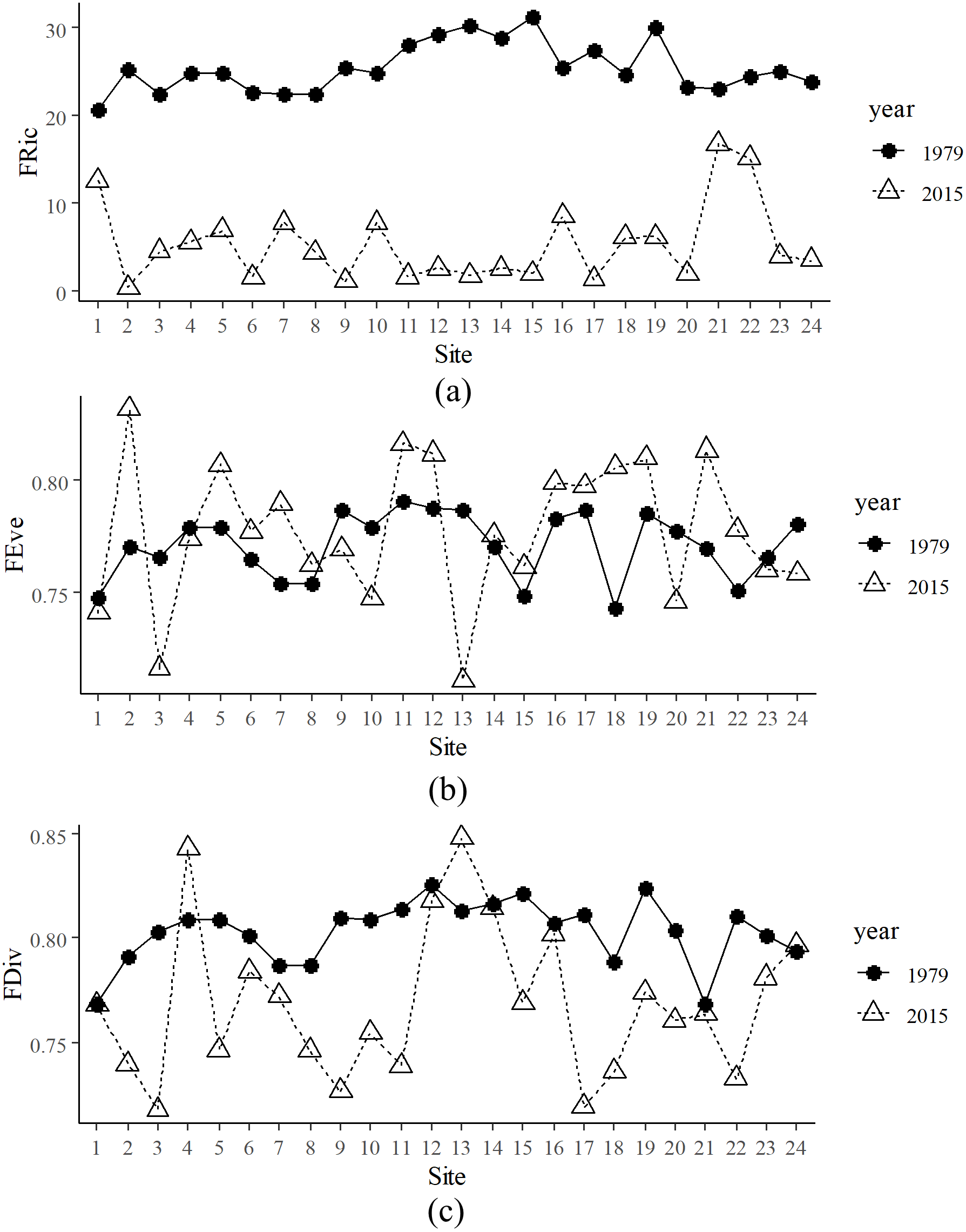



3txt8jmaykhlzm



2



2




Gata Transcription Factors Sox17 And Tfap2c Drive The Human Germ Cell Specification Program Life Science Alliance




Pearson Maths Class 9 Solution Pages 1 50 Flip Pdf Download Fliphtml5



2



9000 Test Report 360 Cal Comp Electronics Thailand



2



Antioxidant Antimicrobial And Cytotoxic Properties As Well As The Phenolic Content Of The Extract From Hancornia Speciosa Gomes
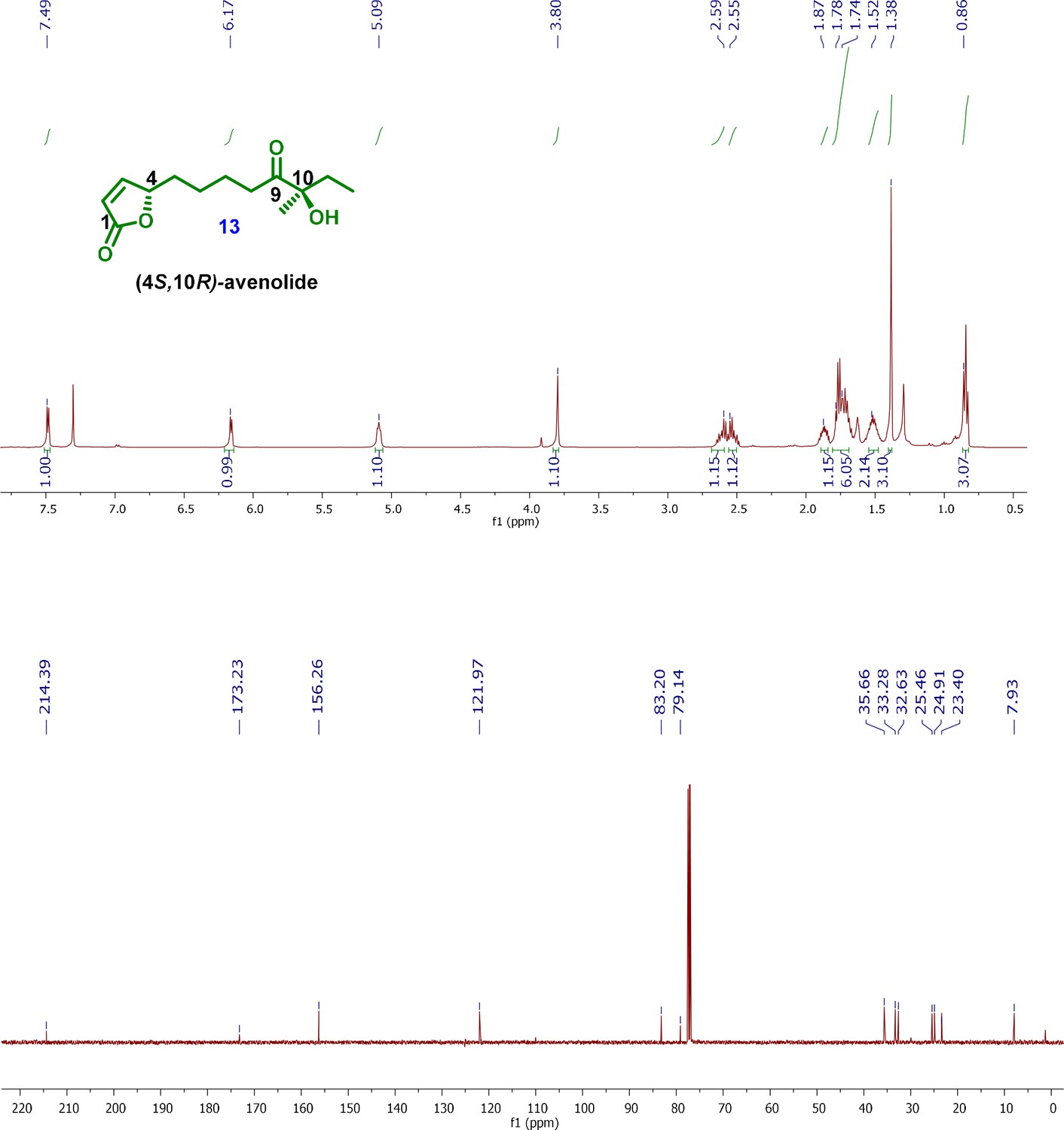



Biochemical Basis For The Regulation Of Biosynthesis Of Antiparasitics By Bacterial Hormones Elife



How To Factorize P 2 Q 2 R 2 2 4 P 2q 2 Quora
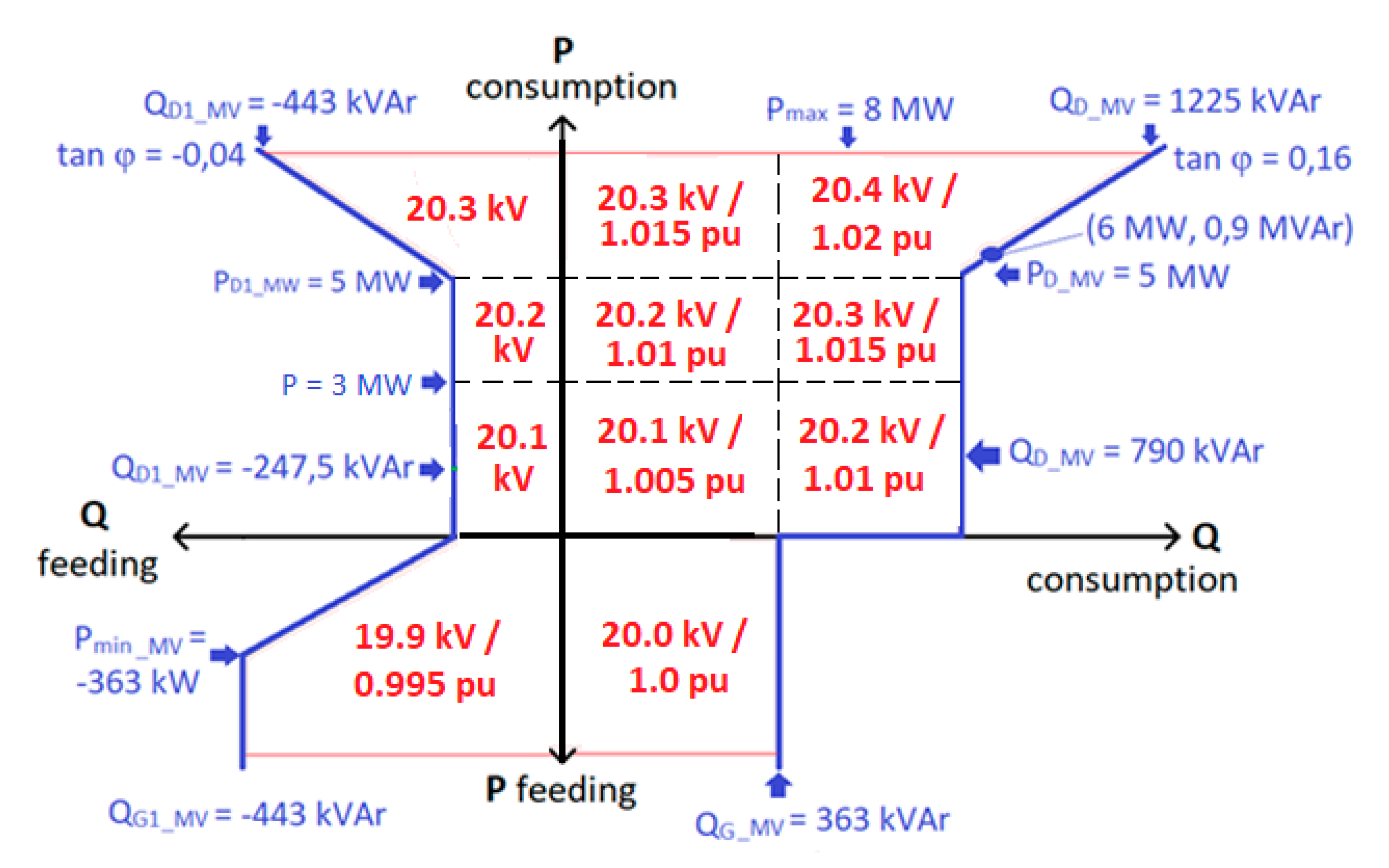



Applied Sciences Free Full Text Solutions To Increase Pv Hosting Capacity And Provision Of Services From Flexible Energy Resources Html




Doppler Radar Analysis Of The Northfield Texas Tornado Of 25 May 1994 In Monthly Weather Review Volume 125 Issue 2 1997




Factorise P Q P Q 125 Brainly In




Factorize P Q P Q 125 Brainly In




Factorize P Q 2 P Q 125
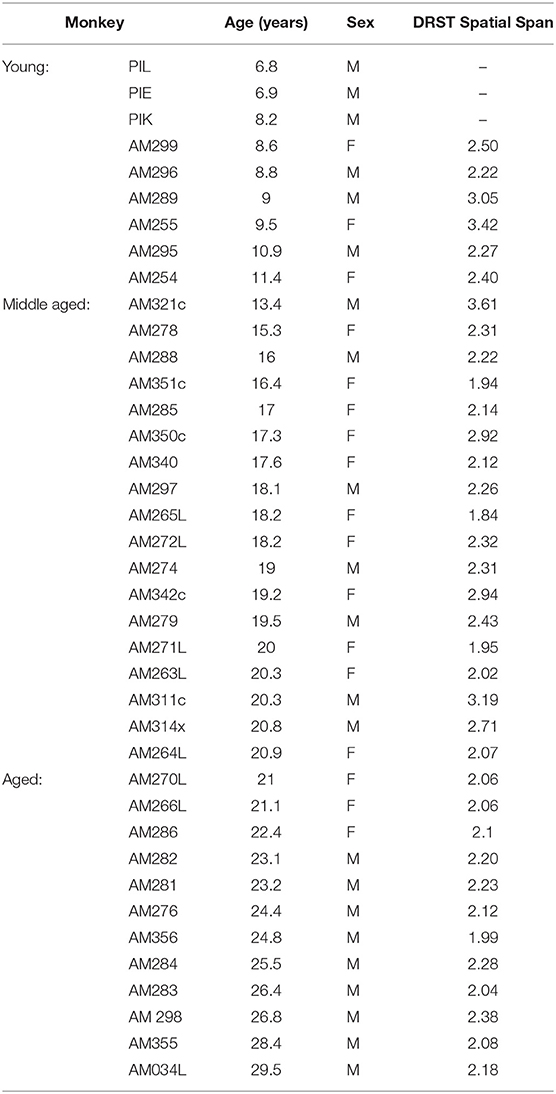



Frontiers Network Models Predict That Pyramidal Neuron Hyperexcitability And Synapse Loss In The Dlpfc Lead To Age Related Spatial Working Memory Impairment In Rhesus Monkeys Frontiers In Computational Neuroscience




Page 2 F3 5 4 5 High Resolution Stock Photography And Images Alamy




A Parkinson S Disease Circrnas Resource Reveals A Link Between Circslc8a1 And Oxidative Stress Embo Molecular Medicine




Factorize P Q 2 P Q 125




Secondary Lesson Plan E Ctlt




Pet Adapted Treatment For Newly Diagnosed Advanced Hodgkin Lymphoma Ahl11 A Randomised Multicentre Non Inferiority Phase 3 Study The Lancet Oncology




Use Straightforward Algebraic Methods And Solve Equations 1 1 Ppt Download
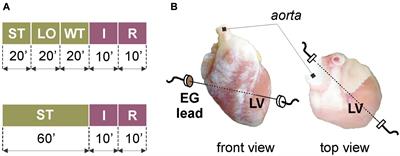



Frontiers Di 4 Anepps Modulates Electrical Activity And Progress Of Myocardial Ischemia In Rabbit Isolated Heart Physiology



2




Factorise P 2q Pr 2 Pq R 2 Youtube




Gata Transcription Factors Sox17 And Tfap2c Drive The Human Germ Cell Specification Program Life Science Alliance




Lt Div Class Quot Relative Mb 10 Md M 0 Quot Gt P Q 2 P Q 125 P Q 2 P Q 125



2



Full Article Xxxiv International Congress Of The European Association Of Poisons Centres And Clinical Toxicologists Eapcct 27 30 May 14 Brussels Belgium



2



1



The Molecular Basis For The Prothrombotic State In Sickle Cell Disease Haematologica



2



2




Ex 14 3 4 Iii Divide 52pqr P Q Q R R P 104pq Q R



Overview Of Salvia Miltiorrhiza As A Potential Therapeutic Agent For Various Diseases An Update On Efficacy And Mechanisms Of Action Document Gale Academic Onefile
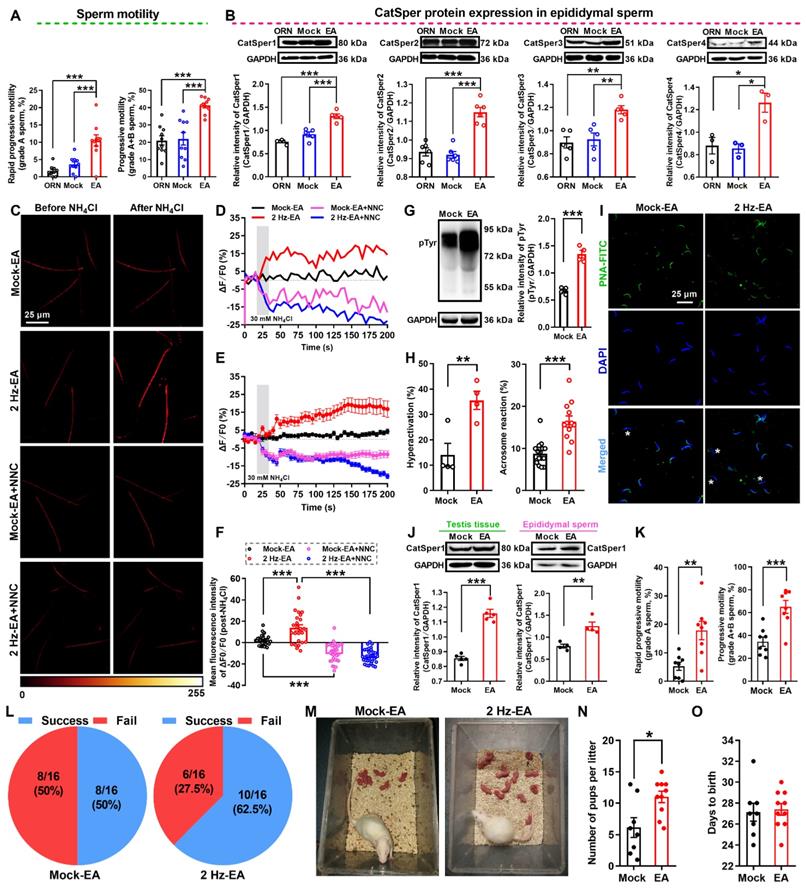



Roles Of Catsper Channels In The Pathogenesis Of Asthenozoospermia And The Therapeutic Effects Of Acupuncture Like Treatment On Asthenozoospermia



2



For M 3 2 Tev We Plot The Gmm Parameter Space In The M Mm 0 Vs M Download Scientific Diagram



2




Factoring Special Binomials



2
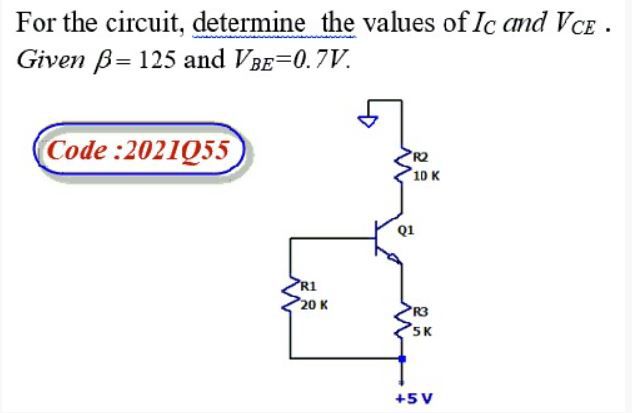



Answered For The Circuit Determine The Values Bartleby




Medicinal Chemistry Strategies For The Development Of Phosphodiesterase 10a Pde10a Inhibitors An Update Of Recent Progress Sciencedirect




Suffolk City Council Meeting Full Agenda June 17 By City Of Suffolk Virginia Issuu
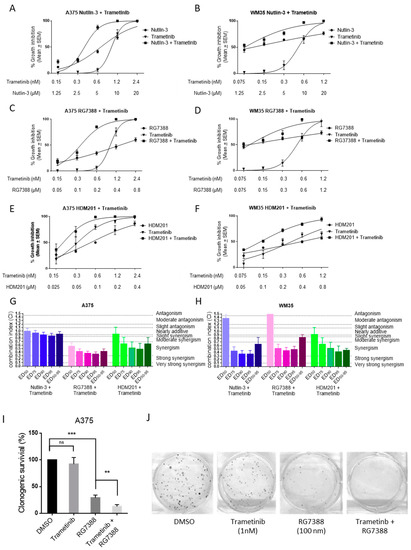



Cancers Free Full Text Atm Dependent Dusp6 Modulation Of P53 Involved In Synergistic Targeting Of Mapk And P53 Pathways With Trametinib And Mdm2 Inhibitors In Cutaneous Melanoma Html



2




Factorise P Q 2 P Q 125 Expertzzz Pls Answer Brainly In



How To Factorize P 2 Q 2 R 2 2 4 P 2q 2 Quora



2



2




Effect Of Mitochondrial Antioxidant Mito Tempo On Burn Induced Cardiac Dysfunction Journal Of The American College Of Surgeons



2




Factorize P Q 2 P Q 125 Youtube




nd Annual Meeting Of The American Thyroid Associationmeeting Abstracts Program Thyroid



Probability Distribution For Mixed Modulus Anomaly Mixing Parameter A Download Scientific Diagram



2




Conditionally Pathogenic Gut Microbes Promote Larval Growth By Increasing Redox Dependent Fat Storage In High Sugar Diet Fed Drosophila Antioxidants Redox Signaling




Lt Div Class Quot Relative Mb 10 Md M 0 Quot Gt P Q 2 P Q 125 P Q 2 P Q 125




Ix Polynomials Factorise P Q 2 p Q 125 Youtube




Asbmr 30th Annual Meeting 1001 1300 08 Journal Of Bone And Mineral Research Wiley Online Library




Abnormal Muscle Mechanosignaling Triggers Cardiomyopathy In Mice With Marfan Syndrome Abstract Europe Pmc



2




Factorise P Q 2 A B 2 P Q A B Maths Factorisation Meritnation Com




Question 4 Page 15 It Is Required To 125 Marks Design A Cold Storage For Storing Homeworklib



2




Obesity And Its Cardio Metabolic Co Morbidities Among Adult Nigerians In A Primary Care Clinic Of A Tertiary Hospital In South Eastern Nigeria Abstract Europe Pmc



0 件のコメント:
コメントを投稿